Package g2301_2400.s2397_maximum_rows_covered_by_columns

Class Solution

  • public class Solution
extends Object
    2397 - Maximum Rows Covered by Columns.

    Medium

    You are given a 0-indexed m x n binary matrix matrix and an integer numSelect, which denotes the number of distinct columns you must select from matrix.

    Let us consider s = {c1, c2, …., cnumSelect} as the set of columns selected by you. A row row is covered by s if:

    • For each cell matrix[row][col] (0 <= col <= n - 1) where matrix[row][col] == 1, col is present in s or,
    • No cell in row has a value of 1.

    You need to choose numSelect columns such that the number of rows that are covered is maximized.

    Return the maximum number of rows that can be covered by a set of numSelect columns.

    Example 1:

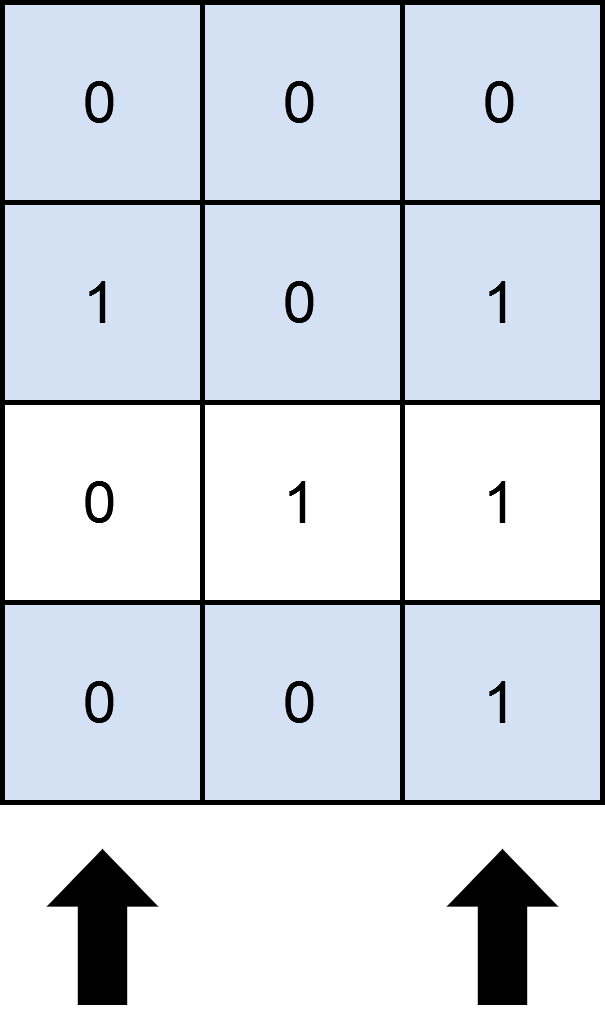
    Input: matrix = [[0,0,0],[1,0,1],[0,1,1],[0,0,1]], numSelect = 2

    Output: 3

    Explanation: One possible way to cover 3 rows is shown in the diagram above.

    We choose s = {0, 2}.

    • Row 0 is covered because it has no occurrences of 1.

    • Row 1 is covered because the columns with value 1, i.e. 0 and 2 are present in s.

    • Row 2 is not covered because matrix[2][1] == 1 but 1 is not present in s.

    • Row 3 is covered because matrix[2][2] == 1 and 2 is present in s.

    Thus, we can cover three rows.

    Note that s = {1, 2} will also cover 3 rows, but it can be shown that no more than three rows can be covered.

    Example 2:

    Input: matrix = [[1],[0]], numSelect = 1

    Output: 2

    Explanation: Selecting the only column will result in both rows being covered since the entire matrix is selected.

    Therefore, we return 2.

    Constraints:

    • m == matrix.length
    • n == matrix[i].length
    • 1 <= m, n <= 12
    • matrix[i][j] is either 0 or 1.
    • 1 <= numSelect <= n

    • Constructor Detail

      • Solution

        public Solution()

    • Method Detail

      • maximumRows

        public int maximumRows​(int[][] matrix,
                       int numSelect)