Package g1601_1700.s1609_even_odd_tree

Class Solution

  • public class Solution
extends Object
    1609 - Even Odd Tree.

    Medium

    A binary tree is named Even-Odd if it meets the following conditions:

    • The root of the binary tree is at level index 0, its children are at level index 1, their children are at level index 2, etc.
    • For every even-indexed level, all nodes at the level have odd integer values in strictly increasing order (from left to right).
    • For every odd-indexed level, all nodes at the level have even integer values in strictly decreasing order (from left to right).

    Given the root of a binary tree, return true if the binary tree is Even-Odd , otherwise return false.

    Example 1:

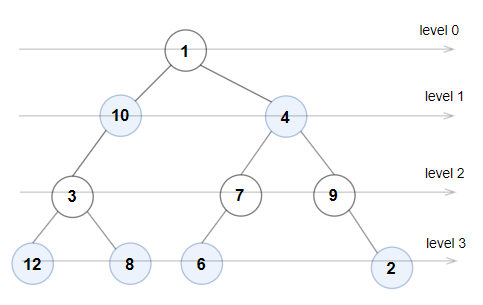
    Input: root = [1,10,4,3,null,7,9,12,8,6,null,null,2]

    Output: true

    Explanation: The node values on each level are:

    Level 0: [1]

    Level 1: [10,4]

    Level 2: [3,7,9]

    Level 3: [12,8,6,2]

    Since levels 0 and 2 are all odd and increasing and levels 1 and 3 are all even and decreasing, the tree is Even-Odd.

    Example 2:

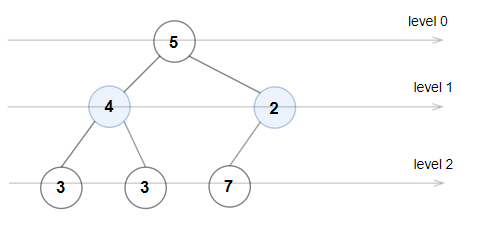
    Input: root = [5,4,2,3,3,7]

    Output: false

    Explanation: The node values on each level are:

    Level 0: [5]

    Level 1: [4,2]

    Level 2: [3,3,7]

    Node values in level 2 must be in strictly increasing order, so the tree is not Even-Odd.

    Example 3:

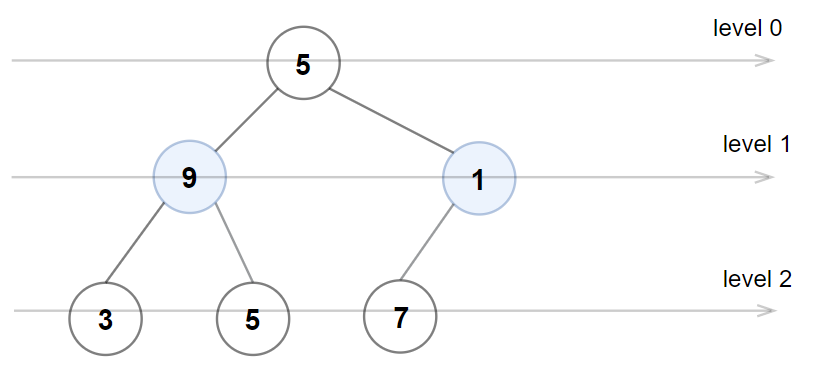
    Input: root = [5,9,1,3,5,7]

    Output: false

    Explanation: Node values in the level 1 should be even integers.

    Constraints:

    • The number of nodes in the tree is in the range [1, 105].
    • 1 <= Node.val <= 106

    • Constructor Detail

      • Solution

        public Solution()

    • Method Detail

      • isEvenOddTree

        public boolean isEvenOddTree​(TreeNode root)