public class Solution
extends Object
778 - Swim in Rising Water\.
Hard
You are given an `n x n` integer matrix `grid` where each value `grid[i][j]` represents the elevation at that point `(i, j)`.
The rain starts to fall. At time `t`, the depth of the water everywhere is `t`. You can swim from a square to another 4-directionally adjacent square if and only if the elevation of both squares individually are at most `t`. You can swim infinite distances in zero time. Of course, you must stay within the boundaries of the grid during your swim.
Return _the least time until you can reach the bottom right square_ `(n - 1, n - 1)` _if you start at the top left square_ `(0, 0)`.
**Example 1:**
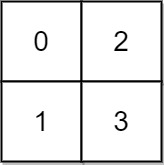
**Input:** grid = \[\[0,2],[1,3]]
**Output:** 3
**Explanation:**
At time 0, you are in grid location (0, 0).
You cannot go anywhere else because 4-directionally adjacent neighbors have a higher elevation than t = 0.
You cannot reach point (1, 1) until time 3.
When the depth of water is 3, we can swim anywhere inside the grid.
**Example 2:**
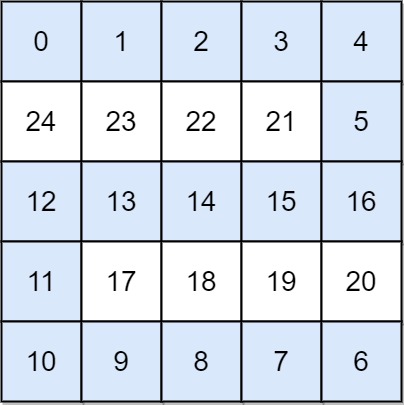
**Input:** grid = \[\[0,1,2,3,4],[24,23,22,21,5],[12,13,14,15,16],[11,17,18,19,20],[10,9,8,7,6]]
**Output:** 16
**Explanation:**
The final route is shown.
We need to wait until time 16 so that (0, 0) and (4, 4) are connected.
**Constraints:**
* `n == grid.length`
* `n == grid[i].length`
* `1 <= n <= 50`
* 0 <= grid[i][j] < n2
* Each value `grid[i][j]` is **unique**.