public class Solution
extends Object
1386 - Cinema Seat Allocation\.
Medium
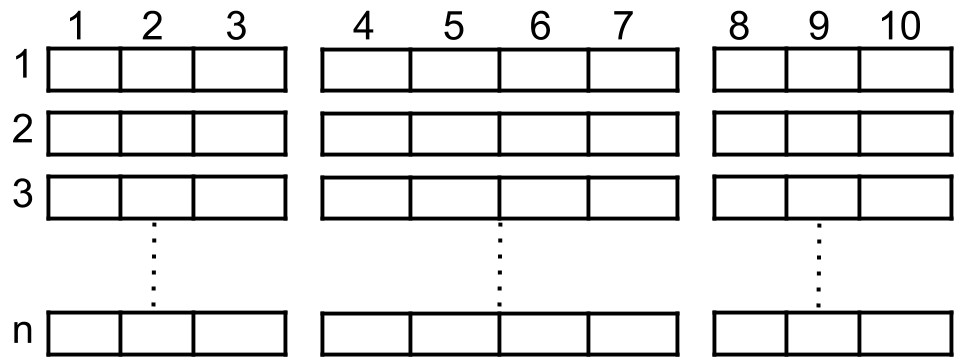
A cinema has `n` rows of seats, numbered from 1 to `n` and there are ten seats in each row, labelled from 1 to 10 as shown in the figure above.
Given the array `reservedSeats` containing the numbers of seats already reserved, for example, `reservedSeats[i] = [3,8]` means the seat located in row **3** and labelled with **8** is already reserved.
_Return the maximum number of four-person groups you can assign on the cinema seats._ A four-person group occupies four adjacent seats **in one single row**. Seats across an aisle (such as [3,3] and [3,4]) are not considered to be adjacent, but there is an exceptional case on which an aisle split a four-person group, in that case, the aisle split a four-person group in the middle, which means to have two people on each side.
**Example 1:**
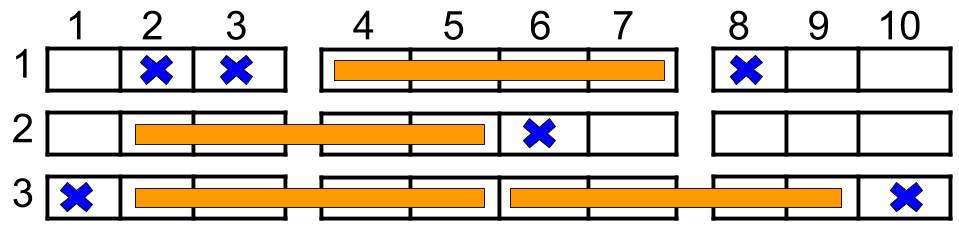
**Input:** n = 3, reservedSeats = \[\[1,2],[1,3],[1,8],[2,6],[3,1],[3,10]]
**Output:** 4
**Explanation:** The figure above shows the optimal allocation for four groups, where seats mark with blue are already reserved and contiguous seats mark with orange are for one group.
**Example 2:**
**Input:** n = 2, reservedSeats = \[\[2,1],[1,8],[2,6]]
**Output:** 2
**Example 3:**
**Input:** n = 4, reservedSeats = \[\[4,3],[1,4],[4,6],[1,7]]
**Output:** 4
**Constraints:**
* `1 <= n <= 10^9`
* `1 <= reservedSeats.length <= min(10*n, 10^4)`
* `reservedSeats[i].length == 2`
* `1 <= reservedSeats[i][0] <= n`
* `1 <= reservedSeats[i][1] <= 10`
* All `reservedSeats[i]` are distinct.