public class Solution
extends Object
1463 - Cherry Pickup II\.
Hard
You are given a `rows x cols` matrix `grid` representing a field of cherries where `grid[i][j]` represents the number of cherries that you can collect from the `(i, j)` cell.
You have two robots that can collect cherries for you:
* **Robot #1** is located at the **top-left corner** `(0, 0)`, and
* **Robot #2** is located at the **top-right corner** `(0, cols - 1)`.
Return _the maximum number of cherries collection using both robots by following the rules below_:
* From a cell `(i, j)`, robots can move to cell `(i + 1, j - 1)`, `(i + 1, j)`, or `(i + 1, j + 1)`.
* When any robot passes through a cell, It picks up all cherries, and the cell becomes an empty cell.
* When both robots stay in the same cell, only one takes the cherries.
* Both robots cannot move outside of the grid at any moment.
* Both robots should reach the bottom row in `grid`.
**Example 1:**
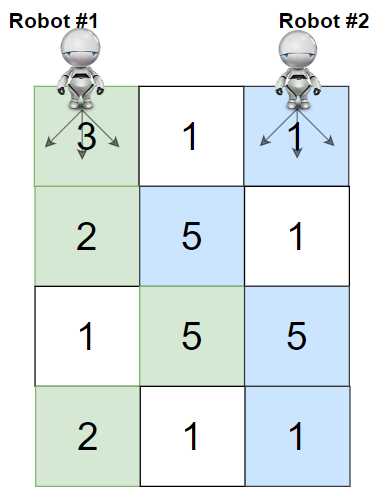
**Input:** grid = \[\[3,1,1],[2,5,1],[1,5,5],[2,1,1]]
**Output:** 24
**Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (3 + 2 + 5 + 2) = 12.
Cherries taken by Robot #2, (1 + 5 + 5 + 1) = 12.
Total of cherries: 12 + 12 = 24.
**Example 2:**
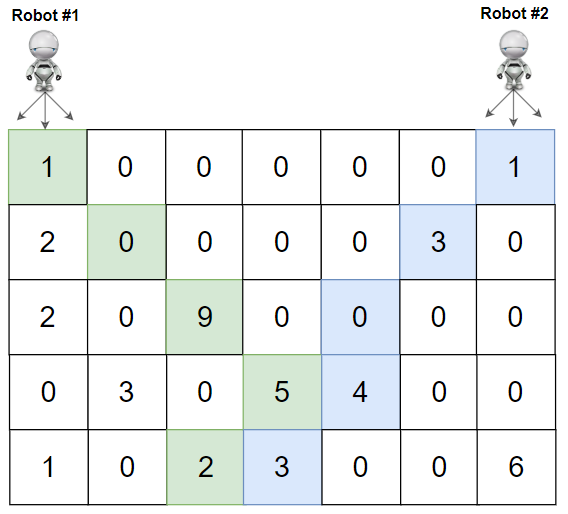
**Input:** grid = \[\[1,0,0,0,0,0,1],[2,0,0,0,0,3,0],[2,0,9,0,0,0,0],[0,3,0,5,4,0,0],[1,0,2,3,0,0,6]]
**Output:** 28
**Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (1 + 9 + 5 + 2) = 17.
Cherries taken by Robot #2, (1 + 3 + 4 + 3) = 11.
Total of cherries: 17 + 11 = 28.
**Constraints:**
* `rows == grid.length`
* `cols == grid[i].length`
* `2 <= rows, cols <= 70`
* `0 <= grid[i][j] <= 100`