public class Solution
extends Object
1766 - Tree of Coprimes\.
Hard
There is a tree (i.e., a connected, undirected graph that has no cycles) consisting of `n` nodes numbered from `0` to `n - 1` and exactly `n - 1` edges. Each node has a value associated with it, and the **root** of the tree is node `0`.
To represent this tree, you are given an integer array `nums` and a 2D array `edges`. Each `nums[i]` represents the ith node's value, and each edges[j] = [uj, vj] represents an edge between nodes uj and vj in the tree.
Two values `x` and `y` are **coprime** if `gcd(x, y) == 1` where `gcd(x, y)` is the **greatest common divisor** of `x` and `y`.
An ancestor of a node `i` is any other node on the shortest path from node `i` to the **root**. A node is **not** considered an ancestor of itself.
Return _an array_ `ans` _of size_ `n`, _where_ `ans[i]` _is the closest ancestor to node_ `i` _such that_ `nums[i]` _and_ `nums[ans[i]]` are **coprime** , or `-1` _if there is no such ancestor_.
**Example 1:**
**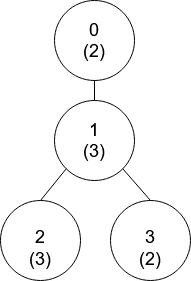**
**Input:** nums = [2,3,3,2], edges = \[\[0,1],[1,2],[1,3]]
**Output:** [-1,0,0,1]
**Explanation:** In the above figure, each node's value is in parentheses.
- Node 0 has no coprime ancestors.
- Node 1 has only one ancestor, node 0. Their values are coprime (gcd(2,3) == 1). - Node 2 has two ancestors, nodes 1 and 0. Node 1's value is not coprime (gcd(3,3) == 3), but node 0's value is (gcd(2,3) == 1), so node 0 is the closest valid ancestor.
- Node 3 has two ancestors, nodes 1 and 0. It is coprime with node 1 (gcd(3,2) == 1), so node 1 is its closest valid ancestor.
**Example 2:**
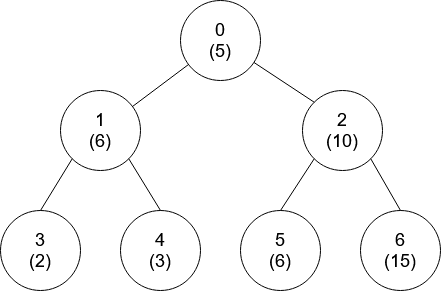
**Input:** nums = [5,6,10,2,3,6,15], edges = \[\[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]]
**Output:** [-1,0,-1,0,0,0,-1]
**Constraints:**
* `nums.length == n`
* `1 <= nums[i] <= 50`
* 1 <= n <= 105
* `edges.length == n - 1`
* `edges[j].length == 2`
* 0 <= uj, vj < n
* uj != vj