public class Solution
extends Object
1895 - Largest Magic Square\.
Medium
A `k x k` **magic square** is a `k x k` grid filled with integers such that every row sum, every column sum, and both diagonal sums are **all equal**. The integers in the magic square **do not have to be distinct**. Every `1 x 1` grid is trivially a **magic square**.
Given an `m x n` integer `grid`, return _the **size** (i.e., the side length_ `k`_) of the **largest magic square** that can be found within this grid_.
**Example 1:**
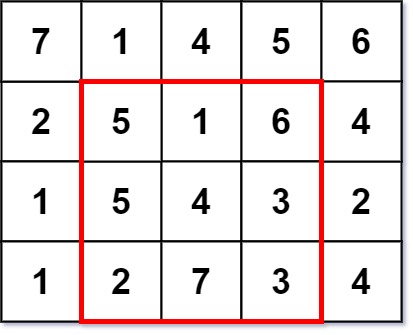
**Input:** grid = \[\[7,1,4,5,6],[2,5,1,6,4],[1,5,4,3,2],[1,2,7,3,4]]
**Output:** 3
**Explanation:** The largest magic square has a size of 3.
Every row sum, column sum, and diagonal sum of this magic square is equal to 12.
- Row sums: 5+1+6 = 5+4+3 = 2+7+3 = 12
- Column sums: 5+5+2 = 1+4+7 = 6+3+3 = 12
- Diagonal sums: 5+4+3 = 6+4+2 = 12
**Example 2:**
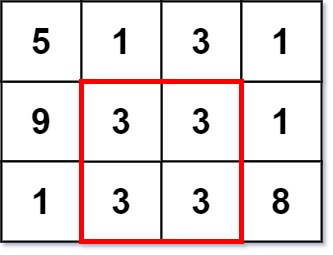
**Input:** grid = \[\[5,1,3,1],[9,3,3,1],[1,3,3,8]]
**Output:** 2
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 50`
* 1 <= grid[i][j] <= 106