Package g2001_2100.s2065_maximum_path_quality_of_a_graph

Class Solution

java.lang.Object

g2001_2100.s2065_maximum_path_quality_of_a_graph.Solution

public class Solution
extends Object

2065 - Maximum Path Quality of a Graph\. Hard There is an **undirected** graph with `n` nodes numbered from `0` to `n - 1` ( **inclusive** ). You are given a **0-indexed** integer array `values` where `values[i]` is the **value** of the ith node. You are also given a **0-indexed** 2D integer array `edges`, where each edges[j] = [uj, vj, timej] indicates that there is an undirected edge between the nodes uj and vj, and it takes timej seconds to travel between the two nodes. Finally, you are given an integer `maxTime`. A **valid** **path** in the graph is any path that starts at node `0`, ends at node `0`, and takes **at most** `maxTime` seconds to complete. You may visit the same node multiple times. The **quality** of a valid path is the **sum** of the values of the **unique nodes** visited in the path (each node's value is added **at most once** to the sum). Return _the **maximum** quality of a valid path_. **Note:** There are **at most four** edges connected to each node. 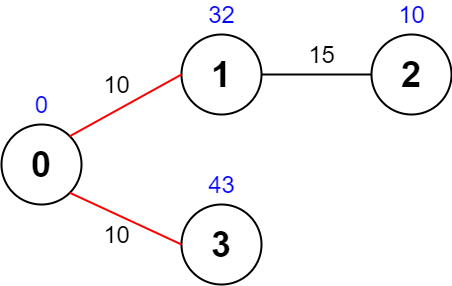**Example 1:**  **Input:** values = [0,32,10,43], edges = \[\[0,1,10],[1,2,15],[0,3,10]], maxTime = 49 **Output:** 75 **Explanation:** One possible path is 0 -> 1 -> 0 -> 3 -> 0. The total time taken is 10 + 10 + 10 + 10 = 40 <= 49. The nodes visited are 0, 1, and 3, giving a maximal path quality of 0 + 32 + 43 = 75. 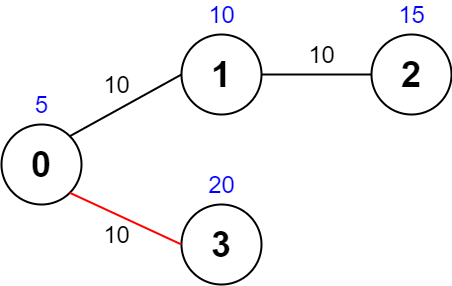**Example 2:**  **Input:** values = [5,10,15,20], edges = \[\[0,1,10],[1,2,10],[0,3,10]], maxTime = 30 **Output:** 25 **Explanation:** One possible path is 0 -> 3 -> 0. The total time taken is 10 + 10 = 20 <= 30. The nodes visited are 0 and 3, giving a maximal path quality of 5 + 20 = 25. 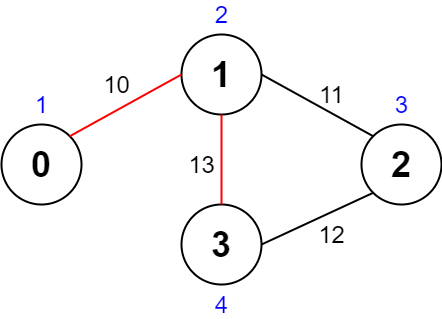**Example 3:**  **Input:** values = [1,2,3,4], edges = \[\[0,1,10],[1,2,11],[2,3,12],[1,3,13]], maxTime = 50 **Output:** 7 **Explanation:** One possible path is 0 -> 1 -> 3 -> 1 -> 0. The total time taken is 10 + 13 + 13 + 10 = 46 <= 50. The nodes visited are 0, 1, and 3, giving a maximal path quality of 1 + 2 + 4 = 7. **Constraints:** * `n == values.length` * `1 <= n <= 1000` * 0 <= values[i] <= 108 * `0 <= edges.length <= 2000` * `edges[j].length == 3` * 0 <= uj < vj <= n - 1 * 10 <= timej, maxTime <= 100 * All the pairs [uj, vj] are **unique**. * There are **at most four** edges connected to each node. * The graph may not be connected.

Constructor Summary

Constructors

Constructor	Description
Solution()

Method Summary

Modifier and Type	Method	Description
int	maximalPathQuality(int[] values, int[][] edges, int maxTime)

Methods inherited from class java.lang.Object

clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

Constructor Detail

Solution

public Solution()

Method Detail

maximalPathQuality

public int maximalPathQuality(int[] values,
                              int[][] edges,
                              int maxTime)