Package g2201_2300.s2201_count_artifacts_that_can_be_extracted

Class Solution

java.lang.Object

g2201_2300.s2201_count_artifacts_that_can_be_extracted.Solution

public class Solution
extends Object

2201 - Count Artifacts That Can Be Extracted\. Medium There is an `n x n` **0-indexed** grid with some artifacts buried in it. You are given the integer `n` and a **0-indexed** 2D integer array `artifacts` describing the positions of the rectangular artifacts where artifacts[i] = [r1i, c1i, r2i, c2i] denotes that the ith artifact is buried in the subgrid where: * (r1i, c1i) is the coordinate of the **top-left** cell of the ith artifact and * (r2i, c2i) is the coordinate of the **bottom-right** cell of the ith artifact. You will excavate some cells of the grid and remove all the mud from them. If the cell has a part of an artifact buried underneath, it will be uncovered. If all the parts of an artifact are uncovered, you can extract it. Given a **0-indexed** 2D integer array `dig` where dig[i] = [ri, ci] indicates that you will excavate the cell (ri, ci), return _the number of artifacts that you can extract_. The test cases are generated such that: * No two artifacts overlap. * Each artifact only covers at most `4` cells. * The entries of `dig` are unique. 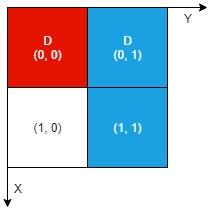**Example 1:**  **Input:** n = 2, artifacts = \[\[0,0,0,0],[0,1,1,1]], dig = \[\[0,0],[0,1]] **Output:** 1 **Explanation:** The different colors represent different artifacts. Excavated cells are labeled with a 'D' in the grid. There is 1 artifact that can be extracted, namely the red artifact. The blue artifact has one part in cell (1,1) which remains uncovered, so we cannot extract it. Thus, we return 1. 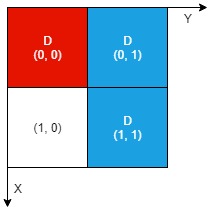**Example 2:**  **Input:** n = 2, artifacts = \[\[0,0,0,0],[0,1,1,1]], dig = \[\[0,0],[0,1],[1,1]] **Output:** 2 **Explanation:** Both the red and blue artifacts have all parts uncovered (labeled with a 'D') and can be extracted, so we return 2. **Constraints:** * `1 <= n <= 1000` * 1 <= artifacts.length, dig.length <= min(n2, 105) * `artifacts[i].length == 4` * `dig[i].length == 2` * 0 <= r1i, c1i, r2i, c2i, ri, ci <= n - 1 * r1i <= r2i * c1i <= c2i * No two artifacts will overlap. * The number of cells covered by an artifact is **at most** `4`. * The entries of `dig` are unique.

Constructor Summary

Constructors

Constructor	Description
Solution()

Method Summary

Modifier and Type	Method	Description
int	digArtifacts(int n, int[][] artifacts, int[][] dig)

Methods inherited from class java.lang.Object

clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

Constructor Detail

Solution

public Solution()

Method Detail

digArtifacts

public int digArtifacts(int n,
                        int[][] artifacts,
                        int[][] dig)