public class Solution
extends Object
2304 - Minimum Path Cost in a Grid\.
Medium
You are given a **0-indexed** `m x n` integer matrix `grid` consisting of **distinct** integers from `0` to `m * n - 1`. You can move in this matrix from a cell to any other cell in the **next** row. That is, if you are in cell `(x, y)` such that `x < m - 1`, you can move to any of the cells `(x + 1, 0)`, `(x + 1, 1)`, ..., `(x + 1, n - 1)`. **Note** that it is not possible to move from cells in the last row.
Each possible move has a cost given by a **0-indexed** 2D array `moveCost` of size `(m * n) x n`, where `moveCost[i][j]` is the cost of moving from a cell with value `i` to a cell in column `j` of the next row. The cost of moving from cells in the last row of `grid` can be ignored.
The cost of a path in `grid` is the **sum** of all values of cells visited plus the **sum** of costs of all the moves made. Return _the **minimum** cost of a path that starts from any cell in the **first** row and ends at any cell in the **last** row._
**Example 1:**
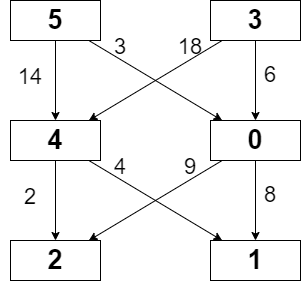
**Input:** grid = \[\[5,3],[4,0],[2,1]], moveCost = \[\[9,8],[1,5],[10,12],[18,6],[2,4],[14,3]]
**Output:** 17
**Explanation:** The path with the minimum possible cost is the path 5 -> 0 -> 1.
- The sum of the values of cells visited is 5 + 0 + 1 = 6.
- The cost of moving from 5 to 0 is 3.
- The cost of moving from 0 to 1 is 8.
So the total cost of the path is 6 + 3 + 8 = 17.
**Example 2:**
**Input:** grid = \[\[5,1,2],[4,0,3]], moveCost = \[\[12,10,15],[20,23,8],[21,7,1],[8,1,13],[9,10,25],[5,3,2]]
**Output:** 6
**Explanation:** The path with the minimum possible cost is the path 2 -> 3.
- The sum of the values of cells visited is 2 + 3 = 5.
- The cost of moving from 2 to 3 is 1.
So the total cost of this path is 5 + 1 = 6.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `2 <= m, n <= 50`
* `grid` consists of distinct integers from `0` to `m * n - 1`.
* `moveCost.length == m * n`
* `moveCost[i].length == n`
* `1 <= moveCost[i][j] <= 100`