Package g0901_1000.s0935_knight_dialer

Class Solution

  • public class Solution
extends Object
    935 - Knight Dialer.

    Medium

    The chess knight has a unique movement , it may move two squares vertically and one square horizontally, or two squares horizontally and one square vertically (with both forming the shape of an L ). The possible movements of chess knight are shown in this diagaram:

    A chess knight can move as indicated in the chess diagram below:

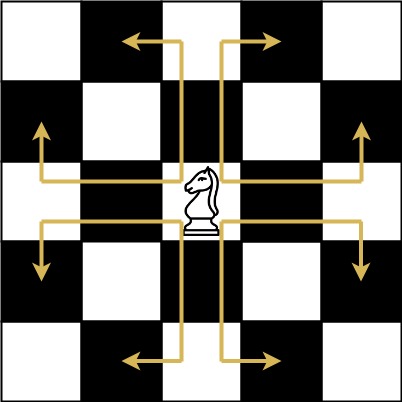
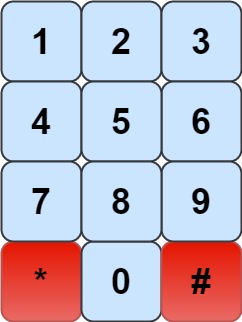
    We have a chess knight and a phone pad as shown below, the knight can only stand on a numeric cell (i.e. blue cell).

    Given an integer n, return how many distinct phone numbers of length n we can dial.

    You are allowed to place the knight on any numeric cell initially and then you should perform n - 1 jumps to dial a number of length n. All jumps should be valid knight jumps.

    As the answer may be very large, return the answer modulo 109 + 7.

    Example 1:

    Input: n = 1

    Output: 10

    Explanation: We need to dial a number of length 1, so placing the knight over any numeric cell of the 10 cells is sufficient.

    Example 2:

    Input: n = 2

    Output: 20

    Explanation: All the valid number we can dial are [04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94]

    Example 3:

    Input: n = 3131

    Output: 136006598

    Explanation: Please take care of the mod.

    Constraints:

    • 1 <= n <= 5000

    • Constructor Detail

      • Solution

        public Solution()

    • Method Detail

      • knightDialer

        public int knightDialer​(int n)