Class Solution
- java.lang.Object
-
- g1601_1700.s1632_rank_transform_of_a_matrix.Solution
-
public class Solution extends Object
1632 - Rank Transform of a Matrix.Hard
Given an
m x nmatrix, return a new matrixanswerwhereanswer[row][col]is the rank ofmatrix[row][col].The rank is an integer that represents how large an element is compared to other elements. It is calculated using the following rules:
- The rank is an integer starting from
1. - If two elements
pandqare in the same row or column , then:- If
p < qthenrank(p) < rank(q) - If
p == qthenrank(p) == rank(q) - If
p > qthenrank(p) > rank(q)
- If
- The rank should be as small as possible.
The test cases are generated so that
answeris unique under the given rules.Example 1:
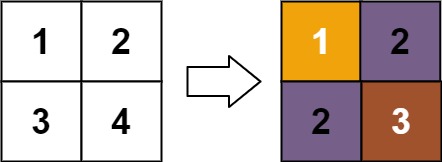
Input: matrix = [[1,2],[3,4]]
Output: [[1,2],[2,3]]
Explanation:
The rank of matrix[0][0] is 1 because it is the smallest integer in its row and column.
The rank of matrix[0][1] is 2 because matrix[0][1] > matrix[0][0] and matrix[0][0] is rank 1.
The rank of matrix[1][0] is 2 because matrix[1][0] > matrix[0][0] and matrix[0][0] is rank 1.
The rank of matrix[1][1] is 3 because matrix[1][1] > matrix[0][1], matrix[1][1] > matrix[1][0], and both matrix[0][1] and matrix[1][0] are rank 2.
Example 2:
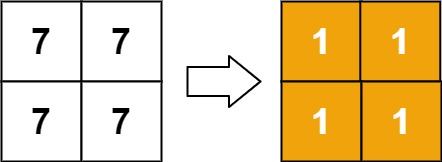
Input: matrix = [[7,7],[7,7]]
Output: [[1,1],[1,1]]
Example 3:
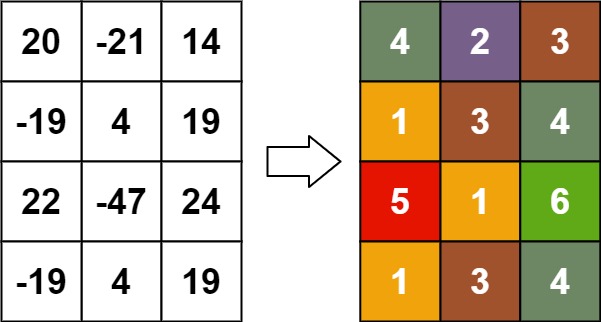
Input: matrix = [[20,-21,14],[-19,4,19],[22,-47,24],[-19,4,19]]
Output: [[4,2,3],[1,3,4],[5,1,6],[1,3,4]]
Constraints:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 500-109 <= matrix[row][col] <= 109
- The rank is an integer starting from
-
-
Constructor Summary
Constructors Constructor Description Solution()
-
Method Summary
All Methods Instance Methods Concrete Methods Modifier and Type Method Description int[][]matrixRankTransform(int[][] matrix)
-