Class Solution
- java.lang.Object
-
- g1901_2000.s1971_find_if_path_exists_in_graph.Solution
-
public class Solution extends Object
1971 - Find if Path Exists in Graph.Easy
There is a bi-directional graph with
nvertices, where each vertex is labeled from0ton - 1( inclusive ). The edges in the graph are represented as a 2D integer arrayedges, where eachedges[i] = [ui, vi]denotes a bi-directional edge between vertexuiand vertexvi. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.You want to determine if there is a valid path that exists from vertex
sourceto vertexdestination.Given
edgesand the integersn,source, anddestination, returntrueif there is a valid path fromsourcetodestination, orfalseotherwise_._Example 1:
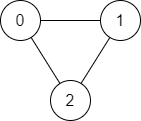
Input: n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
Output: true
Explanation: There are two paths from vertex 0 to vertex 2: - 0 \u2192 1 \u2192 2 - 0 \u2192 2
Example 2:
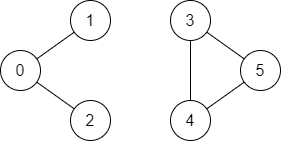
Input: n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
Output: false
Explanation: There is no path from vertex 0 to vertex 5.
Constraints:
1 <= n <= 2 * 1050 <= edges.length <= 2 * 105edges[i].length == 20 <= ui, vi <= n - 1ui != vi0 <= source, destination <= n - 1- There are no duplicate edges.
- There are no self edges.
-
-
Constructor Summary
Constructors Constructor Description Solution()
-