Class Solution
- java.lang.Object
-
- g2401_2500.s2497_maximum_star_sum_of_a_graph.Solution
-
public class Solution extends Object
2497 - Maximum Star Sum of a Graph.Medium
There is an undirected graph consisting of
nnodes numbered from0ton - 1. You are given a 0-indexed integer arrayvalsof lengthnwherevals[i]denotes the value of theithnode.You are also given a 2D integer array
edgeswhereedges[i] = [ai, bi]denotes that there exists an undirected edge connecting nodesaiandbi.A star graph is a subgraph of the given graph having a center node containing
0or more neighbors. In other words, it is a subset of edges of the given graph such that there exists a common node for all edges.The image below shows star graphs with
3and4neighbors respectively, centered at the blue node.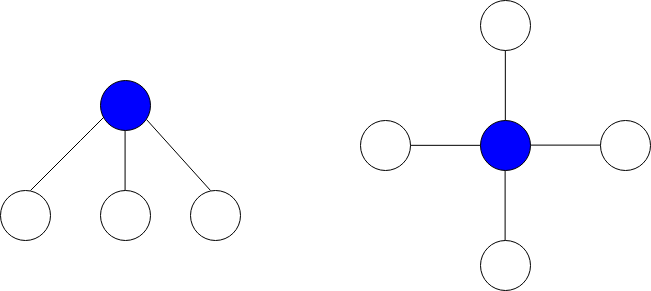
The star sum is the sum of the values of all the nodes present in the star graph.
Given an integer
k, return the maximum star sum of a star graph containing at mostkedges.Example 1:
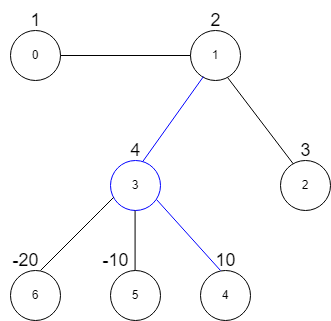
Input: vals = [1,2,3,4,10,-10,-20], edges = [[0,1],[1,2],[1,3],[3,4],[3,5],[3,6]], k = 2
Output: 16
Explanation: The above diagram represents the input graph.
The star graph with the maximum star sum is denoted by blue.
It is centered at 3 and includes its neighbors 1 and 4. It can be shown it is not possible to get a star graph with a sum greater than 16.
Example 2:
Input: vals = [-5], edges = [], k = 0
Output: -5
Explanation: There is only one possible star graph, which is node 0 itself. Hence, we return -5.
Constraints:
n == vals.length1 <= n <= 105-104 <= vals[i] <= 1040 <= edges.length <= min(n * (n - 1) / 2, 105)edges[i].length == 20 <= ai, bi <= n - 1ai != bi0 <= k <= n - 1
-
-
Constructor Summary
Constructors Constructor Description Solution()
-
Method Summary
All Methods Instance Methods Concrete Methods Modifier and Type Method Description intmaxStarSum(int[] nodeValues, int[][] edges, int maxNumberOfEdges)
-