Package g0301_0400.s0310_minimum_height_trees

Class Solution

java.lang.Object

g0301_0400.s0310_minimum_height_trees.Solution

public class Solution
extends Object

310 - Minimum Height Trees\. Medium A tree is an undirected graph in which any two vertices are connected by _exactly_ one path. In other words, any connected graph without simple cycles is a tree. Given a tree of `n` nodes labelled from `0` to `n - 1`, and an array of `n - 1` `edges` where edges[i] = [ai, bi] indicates that there is an undirected edge between the two nodes ai and bi in the tree, you can choose any node of the tree as the root. When you select a node `x` as the root, the result tree has height `h`. Among all possible rooted trees, those with minimum height (i.e. `min(h)`) are called **minimum height trees** (MHTs). Return _a list of all **MHTs'** root labels_. You can return the answer in **any order**. The **height** of a rooted tree is the number of edges on the longest downward path between the root and a leaf. 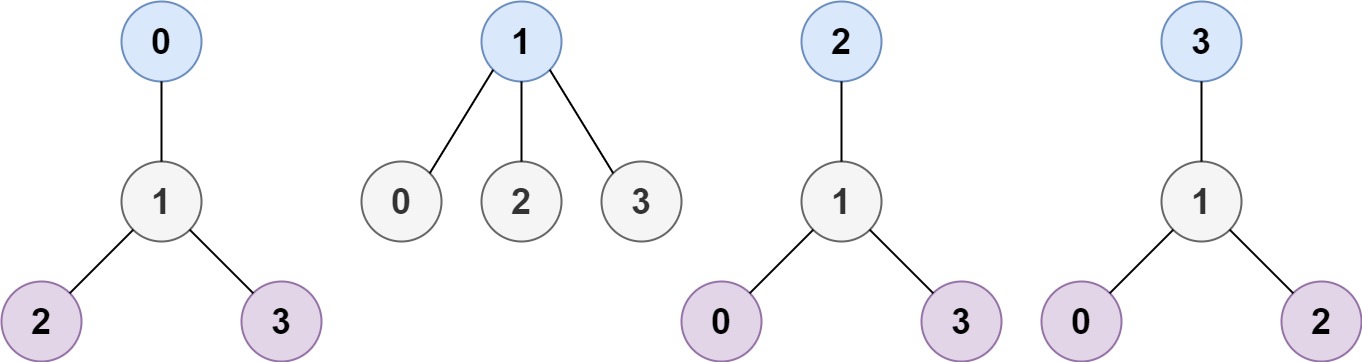**Example 1:**  **Input:** n = 4, edges = \[\[1,0],[1,2],[1,3]] **Output:** [1] **Explanation:** As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT. 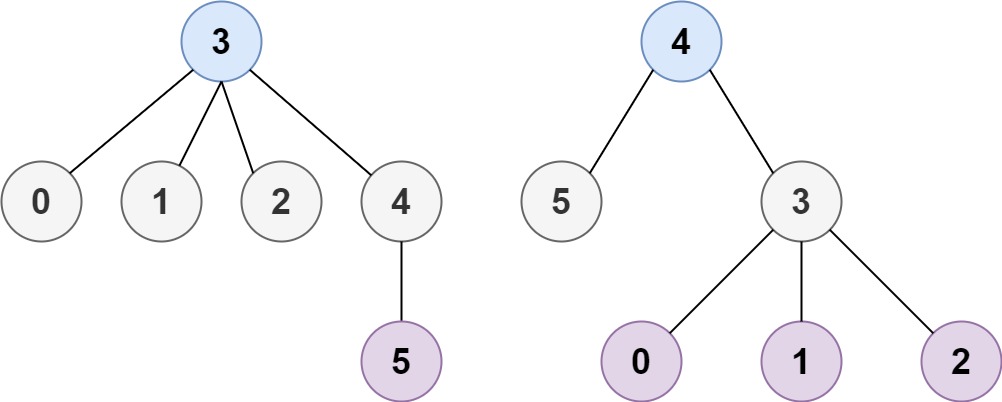**Example 2:**  **Input:** n = 6, edges = \[\[3,0],[3,1],[3,2],[3,4],[5,4]] **Output:** [3,4] **Constraints:** * 1 <= n <= 2 * 104 * `edges.length == n - 1` * 0 <= ai, bi < n * ai != bi * All the pairs (ai, bi) are distinct. * The given input is **guaranteed** to be a tree and there will be **no repeated** edges.

Constructor Summary

Constructors

Constructor	Description
Solution()

Method Summary

Modifier and Type	Method	Description
List<Integer>	findMinHeightTrees(int n, int[][] edges)

Methods inherited from class java.lang.Object

clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

Constructor Details

Solution

public Solution()

Method Details

findMinHeightTrees

public List<Integer> findMinHeightTrees(int n,
 int[][] edges)