Package g0601_0700.s0685_redundant_connection_ii

Class Solution

java.lang.Object

g0601_0700.s0685_redundant_connection_ii.Solution

public class Solution
extends Object

685 - Redundant Connection II\. Hard In this problem, a rooted tree is a **directed** graph such that, there is exactly one node (the root) for which all other nodes are descendants of this node, plus every node has exactly one parent, except for the root node which has no parents. The given input is a directed graph that started as a rooted tree with `n` nodes (with distinct values from `1` to `n`), with one additional directed edge added. The added edge has two different vertices chosen from `1` to `n`, and was not an edge that already existed. The resulting graph is given as a 2D-array of `edges`. Each element of `edges` is a pair [ui, vi] that represents a **directed** edge connecting nodes ui and vi, where ui is a parent of child vi. Return _an edge that can be removed so that the resulting graph is a rooted tree of_ `n` _nodes_. If there are multiple answers, return the answer that occurs last in the given 2D-array. 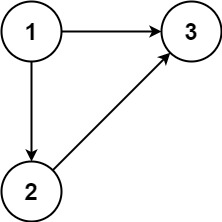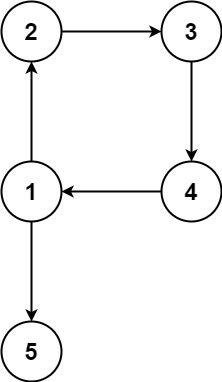**Example 1:**  **Input:** edges = \[\[1,2],[1,3],[2,3]] **Output:** [2,3] **Example 2:**  **Input:** edges = \[\[1,2],[2,3],[3,4],[4,1],[1,5]] **Output:** [4,1] **Constraints:** * `n == edges.length` * `3 <= n <= 1000` * `edges[i].length == 2` * 1 <= ui, vi <= n * ui != vi

Constructor Summary

Constructors

Constructor	Description
Solution()

Method Summary

Modifier and Type	Method	Description
int[]	findRedundantDirectedConnection(int[][] edges)

Methods inherited from class java.lang.Object

clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

Constructor Details

Solution

public Solution()

Method Details

findRedundantDirectedConnection

public int[] findRedundantDirectedConnection(int[][] edges)