Package g0701_0800.s0741_cherry_pickup
Class Solution
java.lang.Object
g0701_0800.s0741_cherry_pickup.Solution
741 - Cherry Pickup\.
Hard
You are given an `n x n` `grid` representing a field of cherries, each cell is one of three possible integers.
* `0` means the cell is empty, so you can pass through,
* `1` means the cell contains a cherry that you can pick up and pass through, or
* `-1` means the cell contains a thorn that blocks your way.
Return _the maximum number of cherries you can collect by following the rules below_:
* Starting at the position `(0, 0)` and reaching `(n - 1, n - 1)` by moving right or down through valid path cells (cells with value `0` or `1`).
* After reaching `(n - 1, n - 1)`, returning to `(0, 0)` by moving left or up through valid path cells.
* When passing through a path cell containing a cherry, you pick it up, and the cell becomes an empty cell `0`.
* If there is no valid path between `(0, 0)` and `(n - 1, n - 1)`, then no cherries can be collected.
**Example 1:**
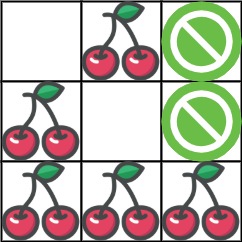
**Input:** grid = \[\[0,1,-1],[1,0,-1],[1,1,1]]
**Output:** 5
**Explanation:** The player started at (0, 0) and went down, down, right right to reach (2, 2). 4 cherries were picked up during this single trip, and the matrix becomes [[0,1,-1],[0,0,-1],[0,0,0]]. Then, the player went left, up, up, left to return home, picking up one more cherry. The total number of cherries picked up is 5, and this is the maximum possible.
**Example 2:**
**Input:** grid = \[\[1,1,-1],[1,-1,1],[-1,1,1]]
**Output:** 0
**Constraints:**
* `n == grid.length`
* `n == grid[i].length`
* `1 <= n <= 50`
* `grid[i][j]` is `-1`, `0`, or `1`.
* `grid[0][0] != -1`
* `grid[n - 1][n - 1] != -1`
-
Constructor Summary
Constructors -
Method Summary
-
Constructor Details
-
Solution
public Solution()
-
-
Method Details
-
cherryPickup
public int cherryPickup(int[][] grid)
-