Package g0801_0900.s0850_rectangle_area_ii

Class Solution

java.lang.Object

g0801_0900.s0850_rectangle_area_ii.Solution

public class Solution
extends Object

850 - Rectangle Area II\. Hard You are given a 2D array of axis-aligned `rectangles`. Each rectangle[i] = [xi1, yi1, xi2, yi2] denotes the ith rectangle where (xi1, yi1) are the coordinates of the **bottom-left corner** , and (xi2, yi2) are the coordinates of the **top-right corner**. Calculate the **total area** covered by all `rectangles` in the plane. Any area covered by two or more rectangles should only be counted **once**. Return _the **total area**_. Since the answer may be too large, return it **modulo** 109 + 7. 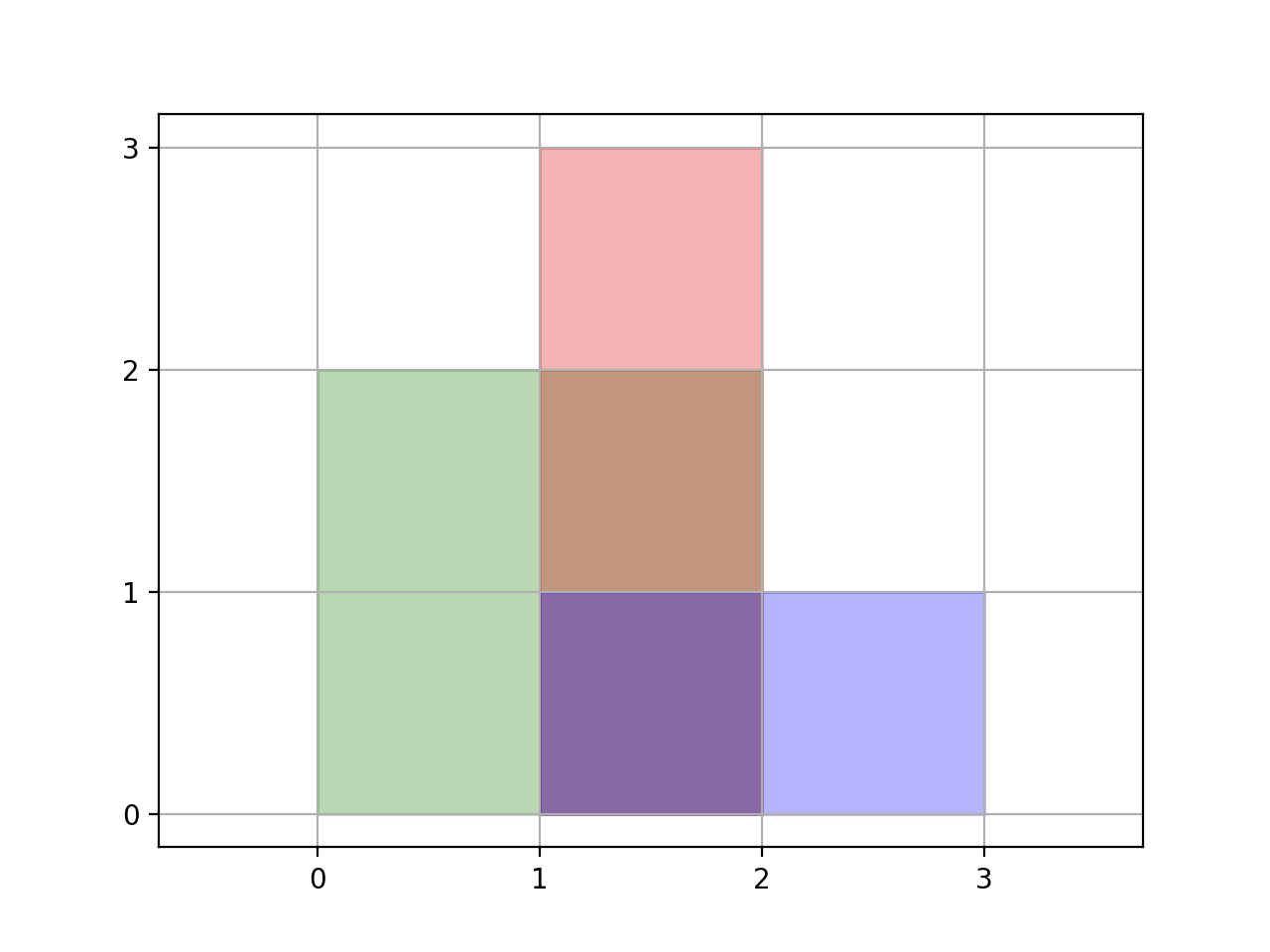**Example 1:**  **Input:** rectangles = \[\[0,0,2,2],[1,0,2,3],[1,0,3,1]] **Output:** 6 **Explanation:** A total area of 6 is covered by all three rectangales, as illustrated in the picture. From (1,1) to (2,2), the green and red rectangles overlap. From (1,0) to (2,3), all three rectangles overlap. **Example 2:** **Input:** rectangles = \[\[0,0,1000000000,1000000000]] **Output:** 49 **Explanation:** The answer is 10¹⁸ modulo (10⁹ + 7), which is 49. **Constraints:** * `1 <= rectangles.length <= 200` * `rectanges[i].length == 4` * 0 <= xi1, yi1, xi2, yi2 <= 109

Constructor Summary

Constructors

Constructor	Description
Solution()

Method Summary

Modifier and Type	Method	Description
int	rectangleArea(int[][] rectangles)

Methods inherited from class java.lang.Object

clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

Constructor Details

Solution

public Solution()

Method Details

rectangleArea

public int rectangleArea(int[][] rectangles)