Package g1201_1300.s1222_queens_that_can_attack_the_king

Class Solution

java.lang.Object

g1201_1300.s1222_queens_that_can_attack_the_king.Solution

public class Solution
extends Object

1222 - Queens That Can Attack the King\. Medium On an **8x8** chessboard, there can be multiple Black Queens and one White King. Given an array of integer coordinates `queens` that represents the positions of the Black Queens, and a pair of coordinates `king` that represent the position of the White King, return the coordinates of all the queens (in any order) that can attack the King. 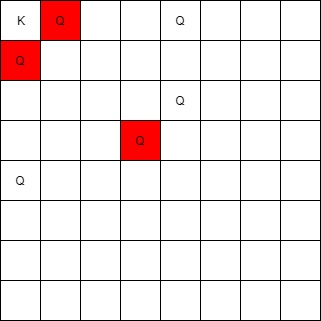**Example 1:**  **Input:** queens = \[\[0,1],[1,0],[4,0],[0,4],[3,3],[2,4]], king = [0,0] **Output:** [[0,1],[1,0],[3,3]] **Explanation:** The queen at [0,1] can attack the king cause they're in the same row. The queen at [1,0] can attack the king cause they're in the same column. The queen at [3,3] can attack the king cause they're in the same diagnal. The queen at [0,4] can't attack the king cause it's blocked by the queen at [0,1]. The queen at [4,0] can't attack the king cause it's blocked by the queen at [1,0]. The queen at [2,4] can't attack the king cause it's not in the same row/column/diagnal as the king. 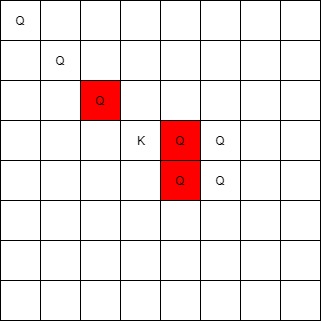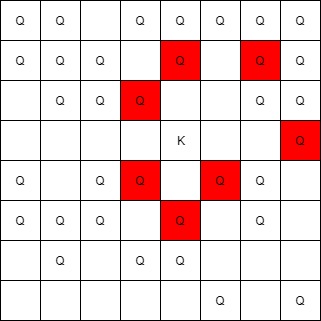**Example 2:** **** **Input:** queens = \[\[0,0],[1,1],[2,2],[3,4],[3,5],[4,4],[4,5]], king = [3,3] **Output:** [[2,2],[3,4],[4,4]] **Example 3:** **** **Input:** queens = \[\[5,6],[7,7],[2,1],[0,7],[1,6],[5,1],[3,7],[0,3],[4,0],[1,2],[6,3],[5,0],[0,4],[2,2],[1,1],[6,4],[5,4],[0,0],[2,6],[4,5],[5,2],[1,4],[7,5],[2,3],[0,5],[4,2],[1,0],[2,7],[0,1],[4,6],[6,1],[0,6],[4,3],[1,7]], king = [3,4] **Output:** [[2,3],[1,4],[1,6],[3,7],[4,3],[5,4],[4,5]] **Constraints:** * `1 <= queens.length <= 63` * `queens[i].length == 2` * `0 <= queens[i][j] < 8` * `king.length == 2` * `0 <= king[0], king[1] < 8` * At most one piece is allowed in a cell.

Constructor Summary

Constructors

Constructor	Description
Solution()

Method Summary

Modifier and Type	Method	Description
void	dfs(Map<Integer,Set<Integer>> queens, int x, int y, List<List<Integer>> result, String direction)
List<List<Integer>>	queensAttacktheKing(int[][] queens, int[] king)

Methods inherited from class java.lang.Object

clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

Constructor Details

Solution

public Solution()

Method Details

queensAttacktheKing

public List<List<Integer>> queensAttacktheKing(int[][] queens,
 int[] king)

dfs

public void dfs(Map<Integer,Set<Integer>> queens,
 int x,
 int y,
 List<List<Integer>> result,
 String direction)