Package g1501_1600.s1514_path_with_maximum_probability

Class Solution

java.lang.Object

g1501_1600.s1514_path_with_maximum_probability.Solution

public class Solution
extends Object

1514 - Path with Maximum Probability\. Medium You are given an undirected weighted graph of `n` nodes (0-indexed), represented by an edge list where `edges[i] = [a, b]` is an undirected edge connecting the nodes `a` and `b` with a probability of success of traversing that edge `succProb[i]`. Given two nodes `start` and `end`, find the path with the maximum probability of success to go from `start` to `end` and return its success probability. If there is no path from `start` to `end`, **return 0**. Your answer will be accepted if it differs from the correct answer by at most **1e-5**. 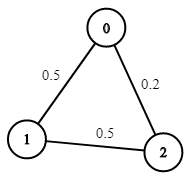**Example 1:** **** **Input:** n = 3, edges = \[\[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2 **Output:** 0.25000 **Explanation:** There are two paths from start to end, one having a probability of success = 0.2 and the other has 0.5 \* 0.5 = 0.25. 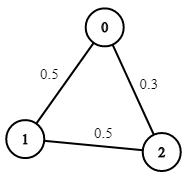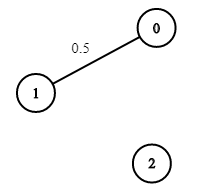**Example 2:** **** **Input:** n = 3, edges = \[\[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2 **Output:** 0.30000 **Example 3:** **** **Input:** n = 3, edges = \[\[0,1]], succProb = [0.5], start = 0, end = 2 **Output:** 0.00000 **Explanation:** There is no path between 0 and 2. **Constraints:** * `2 <= n <= 10^4` * `0 <= start, end < n` * `start != end` * `0 <= a, b < n` * `a != b` * `0 <= succProb.length == edges.length <= 2*10^4` * `0 <= succProb[i] <= 1` * There is at most one edge between every two nodes.

Constructor Summary

Constructors

Constructor	Description
Solution()

Method Summary

Modifier and Type	Method	Description
double	maxProbability(int n, int[][] edges, double[] succProb, int start, int end)

Methods inherited from class java.lang.Object

clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

Constructor Details

Solution

public Solution()

Method Details

maxProbability

public double maxProbability(int n,
 int[][] edges,
 double[] succProb,
 int start,
 int end)