Class Solution
java.lang.Object
g1601_1700.s1601_maximum_number_of_achievable_transfer_requests.Solution
1601 - Maximum Number of Achievable Transfer Requests\.
Hard
We have `n` buildings numbered from `0` to `n - 1`. Each building has a number of employees. It's transfer season, and some employees want to change the building they reside in.
You are given an array `requests` where
requests[i] = [fromi, toi] represents an employee's request to transfer from building fromi to building toi.
**All buildings are full** , so a list of requests is achievable only if for each building, the **net change in employee transfers is zero**. This means the number of employees **leaving** is **equal** to the number of employees **moving in**. For example if `n = 3` and two employees are leaving building `0`, one is leaving building `1`, and one is leaving building `2`, there should be two employees moving to building `0`, one employee moving to building `1`, and one employee moving to building `2`.
Return _the maximum number of achievable requests_.
**Example 1:**
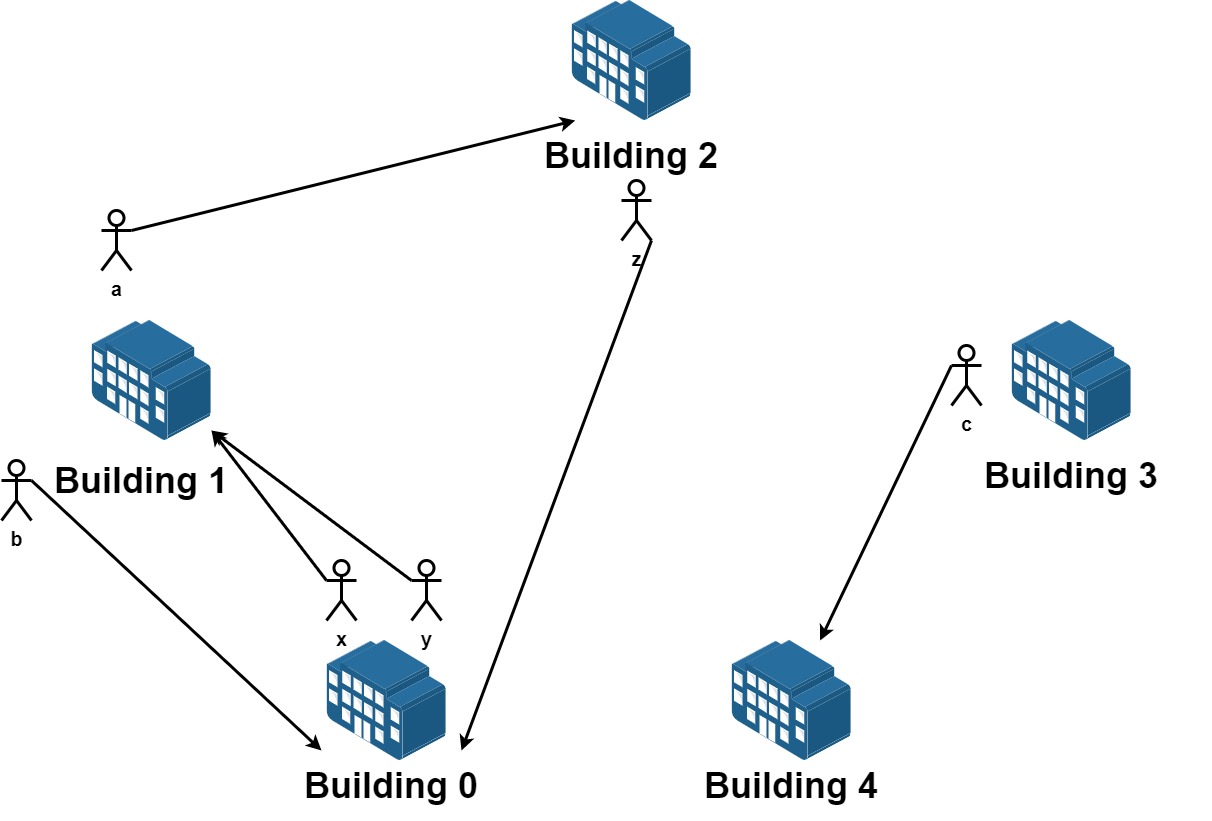
**Input:** n = 5, requests = \[\[0,1],[1,0],[0,1],[1,2],[2,0],[3,4]]
**Output:** 5 **Explantion:** Let's see the requests:
From building 0 we have employees x and y and both want to move to building 1.
From building 1 we have employees a and b and they want to move to buildings 2 and 0 respectively.
From building 2 we have employee z and they want to move to building 0.
From building 3 we have employee c and they want to move to building 4.
From building 4 we don't have any requests.
We can achieve the requests of users x and b by swapping their places.
We can achieve the requests of users y, a and z by swapping the places in the 3 buildings.
**Example 2:**
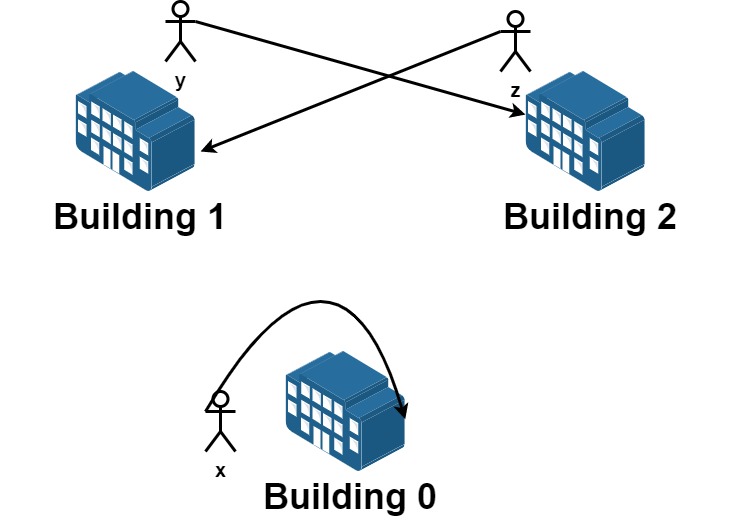
**Input:** n = 3, requests = \[\[0,0],[1,2],[2,1]]
**Output:** 3 **Explantion:** Let's see the requests:
From building 0 we have employee x and they want to stay in the same building 0.
From building 1 we have employee y and they want to move to building 2.
From building 2 we have employee z and they want to move to building 1.
We can achieve all the requests.
**Example 3:**
**Input:** n = 4, requests = \[\[0,3],[3,1],[1,2],[2,0]]
**Output:** 4
**Constraints:**
* `1 <= n <= 20`
* `1 <= requests.length <= 16`
* `requests[i].length == 2`
* 0 <= fromi, toi < n-
Constructor Summary
Constructors -
Method Summary
-
Constructor Details
-
Solution
public Solution()
-
-
Method Details
-
maximumRequests
public int maximumRequests(int n, int[][] requests)
-