Package g1601_1700.s1632_rank_transform_of_a_matrix

Class Solution

java.lang.Object

g1601_1700.s1632_rank_transform_of_a_matrix.Solution

public class Solution
extends Object

1632 - Rank Transform of a Matrix\. Hard Given an `m x n` `matrix`, return _a new matrix_ `answer` _where_ `answer[row][col]` _is the_ _**rank** of_ `matrix[row][col]`. The **rank** is an **integer** that represents how large an element is compared to other elements. It is calculated using the following rules: * The rank is an integer starting from `1`. * If two elements `p` and `q` are in the **same row or column** , then: * If `p < q` then `rank(p) < rank(q)` * If `p == q` then `rank(p) == rank(q)` * If `p > q` then `rank(p) > rank(q)` * The **rank** should be as **small** as possible. The test cases are generated so that `answer` is unique under the given rules. 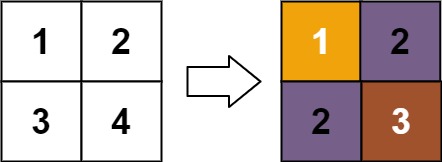**Example 1:**  **Input:** matrix = \[\[1,2],[3,4]] **Output:** [[1,2],[2,3]] **Explanation:** The rank of matrix[0][0] is 1 because it is the smallest integer in its row and column. The rank of matrix[0][1] is 2 because matrix[0][1] > matrix[0][0] and matrix[0][0] is rank 1. The rank of matrix[1][0] is 2 because matrix[1][0] > matrix[0][0] and matrix[0][0] is rank 1. The rank of matrix[1][1] is 3 because matrix[1][1] > matrix[0][1], matrix[1][1] > matrix[1][0], and both matrix[0][1] and matrix[1][0] are rank 2. 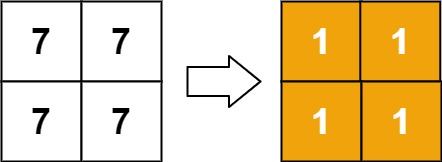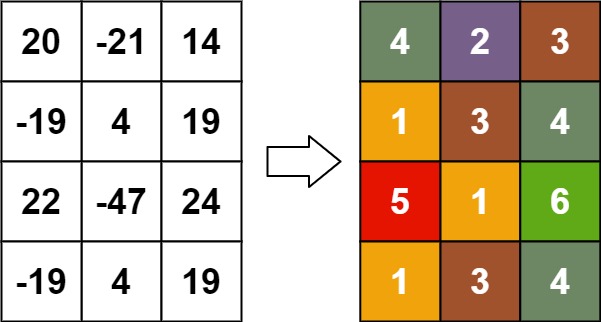**Example 2:**  **Input:** matrix = \[\[7,7],[7,7]] **Output:** [[1,1],[1,1]] **Example 3:**  **Input:** matrix = \[\[20,-21,14],[-19,4,19],[22,-47,24],[-19,4,19]] **Output:** [[4,2,3],[1,3,4],[5,1,6],[1,3,4]] **Constraints:** * `m == matrix.length` * `n == matrix[i].length` * `1 <= m, n <= 500` * -109 <= matrix[row][col] <= 109

Constructor Summary

Constructors

Constructor	Description
Solution()

Method Summary

Modifier and Type	Method	Description
int[][]	matrixRankTransform(int[][] matrix)

Methods inherited from class java.lang.Object

clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

Constructor Details

Solution

public Solution()

Method Details

matrixRankTransform

public int[][] matrixRankTransform(int[][] matrix)