Package g1601_1700.s1659_maximize_grid_happiness

Class Solution

java.lang.Object

g1601_1700.s1659_maximize_grid_happiness.Solution

public class Solution
extends Object

1659 - Maximize Grid Happiness\. Hard You are given four integers, `m`, `n`, `introvertsCount`, and `extrovertsCount`. You have an `m x n` grid, and there are two types of people: introverts and extroverts. There are `introvertsCount` introverts and `extrovertsCount` extroverts. You should decide how many people you want to live in the grid and assign each of them one grid cell. Note that you **do not** have to have all the people living in the grid. The **happiness** of each person is calculated as follows: * Introverts **start** with `120` happiness and **lose** `30` happiness for each neighbor (introvert or extrovert). * Extroverts **start** with `40` happiness and **gain** `20` happiness for each neighbor (introvert or extrovert). Neighbors live in the directly adjacent cells north, east, south, and west of a person's cell. The **grid happiness** is the **sum** of each person's happiness. 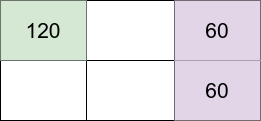Return _the **maximum possible grid happiness**._ **Example 1:**  **Input:** m = 2, n = 3, introvertsCount = 1, extrovertsCount = 2 **Output:** 240 **Explanation:** Assume the grid is 1-indexed with coordinates (row, column). We can put the introvert in cell (1,1) and put the extroverts in cells (1,3) and (2,3). - Introvert at (1,1) happiness: 120 (starting happiness) - (0 \* 30) (0 neighbors) = 120 - Extrovert at (1,3) happiness: 40 (starting happiness) + (1 \* 20) (1 neighbor) = 60 - Extrovert at (2,3) happiness: 40 (starting happiness) + (1 \* 20) (1 neighbor) = 60 The grid happiness is 120 + 60 + 60 = 240. The above figure shows the grid in this example with each person's happiness. The introvert stays in the light green cell while the extroverts live on the light purple cells. **Example 2:** **Input:** m = 3, n = 1, introvertsCount = 2, extrovertsCount = 1 **Output:** 260 **Explanation:** Place the two introverts in (1,1) and (3,1) and the extrovert at (2,1). - Introvert at (1,1) happiness: 120 (starting happiness) - (1 \* 30) (1 neighbor) = 90 - Extrovert at (2,1) happiness: 40 (starting happiness) + (2 \* 20) (2 neighbors) = 80 - Introvert at (3,1) happiness: 120 (starting happiness) - (1 \* 30) (1 neighbor) = 90 The grid happiness is 90 + 80 + 90 = 260. **Example 3:** **Input:** m = 2, n = 2, introvertsCount = 4, extrovertsCount = 0 **Output:** 240 **Constraints:** * `1 <= m, n <= 5` * `0 <= introvertsCount, extrovertsCount <= min(m * n, 6)`

Constructor Summary

Constructors

Constructor	Description
Solution()

Method Summary

Modifier and Type	Method	Description
int	getMaxGridHappiness(int m, int n, int introvertsCount, int extrovertsCount)

Methods inherited from class java.lang.Object

clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

Constructor Details

Solution

public Solution()

Method Details

getMaxGridHappiness

public int getMaxGridHappiness(int m,
 int n,
 int introvertsCount,
 int extrovertsCount)