Package g1801_1900.s1819_number_of_different_subsequences_gcds

Class Solution

java.lang.Object

g1801_1900.s1819_number_of_different_subsequences_gcds.Solution

public class Solution
extends Object

1819 - Number of Different Subsequences GCDs\. Hard You are given an array `nums` that consists of positive integers. The **GCD** of a sequence of numbers is defined as the greatest integer that divides **all** the numbers in the sequence evenly. * For example, the GCD of the sequence `[4,6,16]` is `2`. A **subsequence** of an array is a sequence that can be formed by removing some elements (possibly none) of the array. * For example, `[2,5,10]` is a subsequence of `[1,2,1, **2** ,4,1, **5** , **10** ]`. Return _the **number** of **different** GCDs among all **non-empty** subsequences of_ `nums`. 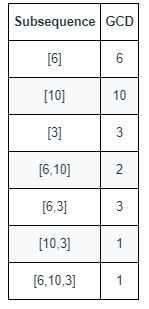**Example 1:**  **Input:** nums = [6,10,3] **Output:** 5 **Explanation:** The figure shows all the non-empty subsequences and their GCDs. The different GCDs are 6, 10, 3, 2, and 1. **Example 2:** **Input:** nums = [5,15,40,5,6] **Output:** 7 **Constraints:** * 1 <= nums.length <= 105 * 1 <= nums[i] <= 2 * 105

Constructor Summary

Constructors

Constructor	Description
Solution()

Method Summary

Modifier and Type	Method	Description
int	countDifferentSubsequenceGCDs(int[] nums)

Methods inherited from class java.lang.Object

clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

Constructor Details

Solution

public Solution()

Method Details

countDifferentSubsequenceGCDs

public int countDifferentSubsequenceGCDs(int[] nums)