Package g1901_2000.s1932_merge_bsts_to_create_single_bst

Class Solution

java.lang.Object

g1901_2000.s1932_merge_bsts_to_create_single_bst.Solution

public class Solution
extends Object

1932 - Merge BSTs to Create Single BST\. Hard You are given `n` **BST (binary search tree) root nodes** for `n` separate BSTs stored in an array `trees` ( **0-indexed** ). Each BST in `trees` has **at most 3 nodes** , and no two roots have the same value. In one operation, you can: * Select two **distinct** indices `i` and `j` such that the value stored at one of the **leaves** of `trees[i]` is equal to the **root value** of `trees[j]`. * Replace the leaf node in `trees[i]` with `trees[j]`. * Remove `trees[j]` from `trees`. Return _the **root** of the resulting BST if it is possible to form a valid BST after performing_ `n - 1` _operations, or_ `null` _if it is impossible to create a valid BST_. A BST (binary search tree) is a binary tree where each node satisfies the following property: * Every node in the node's left subtree has a value **strictly less** than the node's value. * Every node in the node's right subtree has a value **strictly greater** than the node's value. A leaf is a node that has no children. 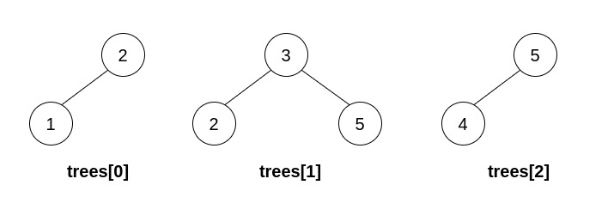**Example 1:**  **Input:** trees = \[\[2,1],[3,2,5],[5,4]] **Output:** [3,2,5,1,null,4] **Explanation:** In the first operation, pick i=1 and j=0, and merge trees[0] into trees[1]. Delete trees[0], so trees = \[\[3,2,5,1],[5,4]]. 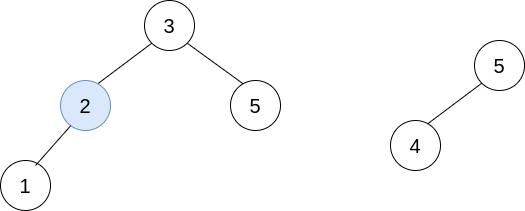 In the second operation, pick i=0 and j=1, and merge trees[1] into trees[0]. Delete trees[1], so trees = \[\[3,2,5,1,null,4]]. 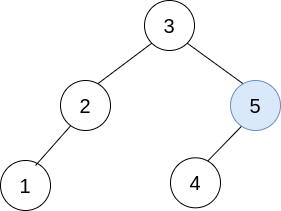 The resulting tree, shown above, is a valid BST, so return its root. 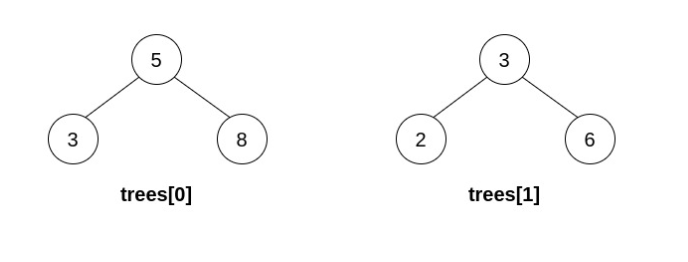**Example 2:**  **Input:** trees = \[\[5,3,8],[3,2,6]] **Output:** [] **Explanation:** Pick i=0 and j=1 and merge trees[1] into trees[0]. Delete trees[1], so trees = \[\[5,3,8,2,6]]. 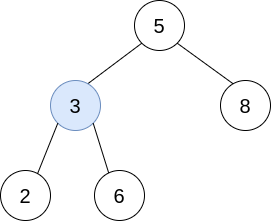 The resulting tree is shown above. This is the only valid operation that can be performed, but the resulting tree is not a valid BST, so return null. 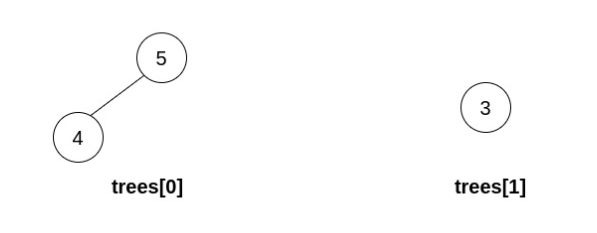**Example 3:**  **Input:** trees = \[\[5,4],[3]] **Output:** [] **Explanation:** It is impossible to perform any operations. **Constraints:** * `n == trees.length` * 1 <= n <= 5 * 104 * The number of nodes in each tree is in the range `[1, 3]`. * Each node in the input may have children but no grandchildren. * No two roots of `trees` have the same value. * All the trees in the input are **valid BSTs**. * 1 <= TreeNode.val <= 5 * 104.

Constructor Summary

Constructors

Constructor	Description
Solution()

Method Summary

Modifier and Type	Method	Description
TreeNode	canMerge(List<TreeNode> trees)

Methods inherited from class java.lang.Object

clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

Constructor Details

Solution

public Solution()

Method Details

canMerge

public TreeNode canMerge(List<TreeNode> trees)