Class Solution
java.lang.Object
g1901_2000.s1937_maximum_number_of_points_with_cost.Solution
1937 - Maximum Number of Points with Cost\.
Medium
You are given an `m x n` integer matrix `points` ( **0-indexed** ). Starting with `0` points, you want to **maximize** the number of points you can get from the matrix.
To gain points, you must pick one cell in **each row**. Picking the cell at coordinates `(r, c)` will **add** `points[r][c]` to your score.
However, you will lose points if you pick a cell too far from the cell that you picked in the previous row. For every two adjacent rows `r` and `r + 1` (where `0 <= r < m - 1`), picking cells at coordinates
(r, c1) and (r + 1, c2) will **subtract** abs(c1 - c2) from your score.
Return _the **maximum** number of points you can achieve_.
`abs(x)` is defined as:
* `x` for `x >= 0`.
* `-x` for `x < 0`.
**Example 1:**
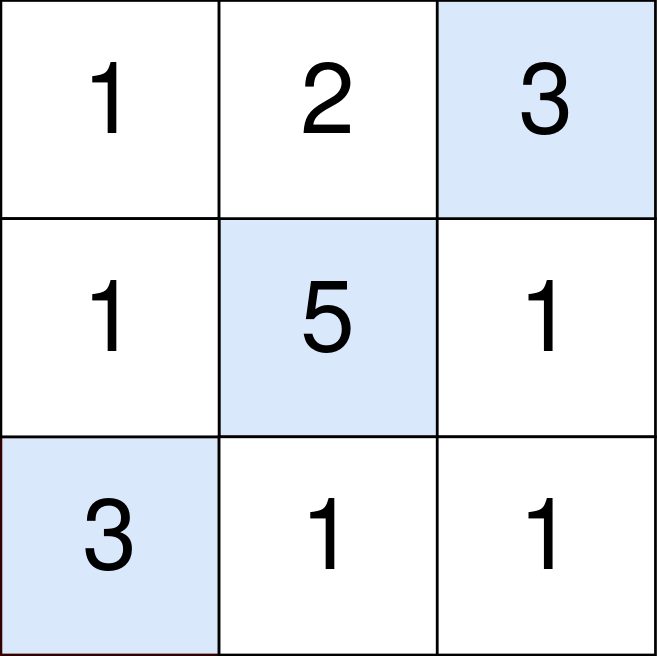
**Input:** points = \[\[1,2,3],[1,5,1],[3,1,1]]
**Output:** 9
**Explanation:**
The blue cells denote the optimal cells to pick, which have coordinates (0, 2), (1, 1), and (2, 0).
You add 3 + 5 + 3 = 11 to your score.
However, you must subtract abs(2 - 1) + abs(1 - 0) = 2 from your score.
Your final score is 11 - 2 = 9.
**Example 2:**
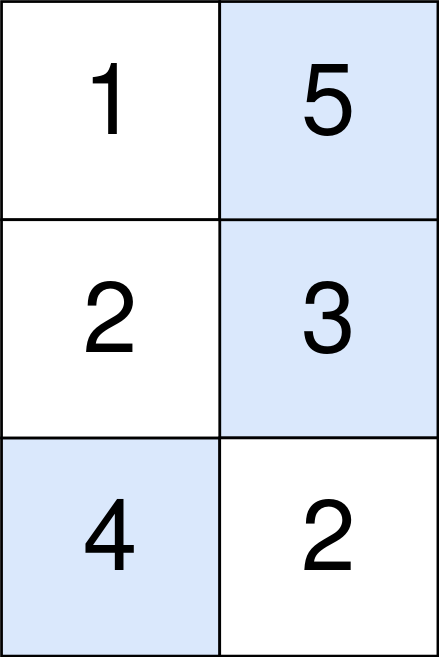
**Input:** points = \[\[1,5],[2,3],[4,2]]
**Output:** 11
**Explanation:**
The blue cells denote the optimal cells to pick, which have coordinates (0, 1), (1, 1), and (2, 0).
You add 5 + 3 + 4 = 12 to your score.
However, you must subtract abs(1 - 1) + abs(1 - 0) = 1 from your score.
Your final score is 12 - 1 = 11.
**Constraints:**
* `m == points.length`
* `n == points[r].length`
* 1 <= m, n <= 105
* 1 <= m * n <= 105
* 0 <= points[r][c] <= 105-
Constructor Summary
Constructors -
Method Summary
-
Constructor Details
-
Solution
public Solution()
-
-
Method Details
-
maxPoints
public long maxPoints(int[][] points)
-