Package g1901_2000.s1943_describe_the_painting

Class Solution

java.lang.Object

g1901_2000.s1943_describe_the_painting.Solution

public class Solution
extends Object

1943 - Describe the Painting\. Medium There is a long and thin painting that can be represented by a number line. The painting was painted with multiple overlapping segments where each segment was painted with a **unique** color. You are given a 2D integer array `segments`, where segments[i] = [starti, endi, colori] represents the **half-closed segment** [starti, endi) with colori as the color. The colors in the overlapping segments of the painting were **mixed** when it was painted. When two or more colors mix, they form a new color that can be represented as a **set** of mixed colors. * For example, if colors `2`, `4`, and `6` are mixed, then the resulting mixed color is `{2,4,6}`. For the sake of simplicity, you should only output the **sum** of the elements in the set rather than the full set. You want to **describe** the painting with the **minimum** number of non-overlapping **half-closed segments** of these mixed colors. These segments can be represented by the 2D array `painting` where painting[j] = [leftj, rightj, mixj] describes a **half-closed segment** [leftj, rightj) with the mixed color **sum** of mixj. * For example, the painting created with `segments = \[\[1,4,5],[1,7,7]]` can be described by `painting = \[\[1,4,12],[4,7,7]]` because: * `[1,4)` is colored `{5,7}` (with a sum of `12`) from both the first and second segments. * `[4,7)` is colored `{7}` from only the second segment. Return _the 2D array_ `painting` _describing the finished painting (excluding any parts that are **not** painted). You may return the segments in **any order**_. A **half-closed segment** `[a, b)` is the section of the number line between points `a` and `b` **including** point `a` and **not including** point `b`. 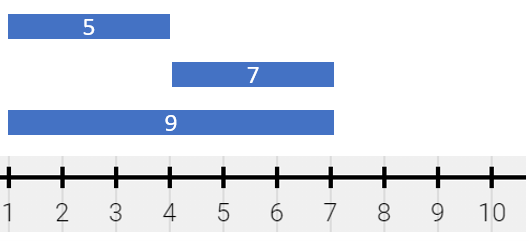**Example 1:**  **Input:** segments = \[\[1,4,5],[4,7,7],[1,7,9]] **Output:** [[1,4,14],[4,7,16]] **Explanation:** The painting can be described as follows: - [1,4) is colored {5,9} (with a sum of 14) from the first and third segments. - [4,7) is colored {7,9} (with a sum of 16) from the second and third segments. 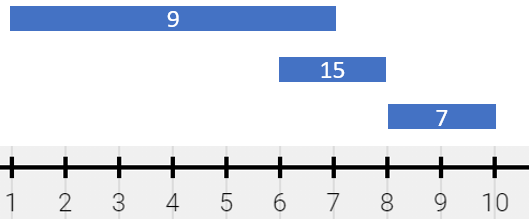**Example 2:**  **Input:** segments = \[\[1,7,9],[6,8,15],[8,10,7]] **Output:** [[1,6,9],[6,7,24],[7,8,15],[8,10,7]] **Explanation:** The painting can be described as follows: - [1,6) is colored 9 from the first segment. - [6,7) is colored {9,15} (with a sum of 24) from the first and second segments. - [7,8) is colored 15 from the second segment. - [8,10) is colored 7 from the third segment. 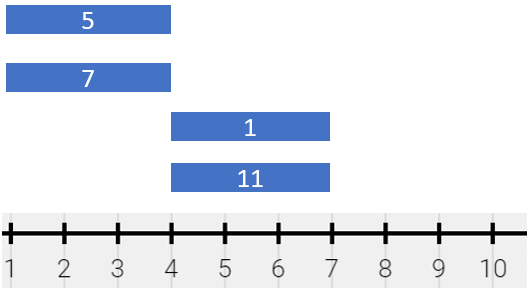**Example 3:**  **Input:** segments = \[\[1,4,5],[1,4,7],[4,7,1],[4,7,11]] **Output:** [[1,4,12],[4,7,12]] **Explanation:** The painting can be described as follows: - [1,4) is colored {5,7} (with a sum of 12) from the first and second segments. - [4,7) is colored {1,11} (with a sum of 12) from the third and fourth segments. Note that returning a single segment [1,7) is incorrect because the mixed color sets are different. **Constraints:** * 1 <= segments.length <= 2 * 104 * `segments[i].length == 3` * 1 <= starti < endi <= 105 * 1 <= colori <= 109 * Each colori is distinct.

Constructor Summary

Constructors

Constructor	Description
Solution()

Method Summary

Modifier and Type	Method	Description
List<List<Long>>	splitPainting(int[][] segments)

Methods inherited from class java.lang.Object

clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

Constructor Details

Solution

public Solution()

Method Details

splitPainting

public List<List<Long>> splitPainting(int[][] segments)