Package g2001_2100.s2017_grid_game

Class Solution

java.lang.Object

g2001_2100.s2017_grid_game.Solution

public class Solution
extends Object

2017 - Grid Game\. Medium You are given a **0-indexed** 2D array `grid` of size `2 x n`, where `grid[r][c]` represents the number of points at position `(r, c)` on the matrix. Two robots are playing a game on this matrix. Both robots initially start at `(0, 0)` and want to reach `(1, n-1)`. Each robot may only move to the **right** (`(r, c)` to `(r, c + 1)`) or **down** (`(r, c)` to `(r + 1, c)`). At the start of the game, the **first** robot moves from `(0, 0)` to `(1, n-1)`, collecting all the points from the cells on its path. For all cells `(r, c)` traversed on the path, `grid[r][c]` is set to `0`. Then, the **second** robot moves from `(0, 0)` to `(1, n-1)`, collecting the points on its path. Note that their paths may intersect with one another. The **first** robot wants to **minimize** the number of points collected by the **second** robot. In contrast, the **second** robot wants to **maximize** the number of points it collects. 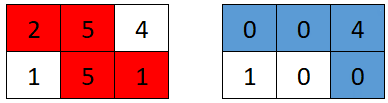If both robots play **optimally** , return _the **number of points** collected by the **second** robot._ **Example 1:**  **Input:** grid = \[\[2,5,4],[1,5,1]] **Output:** 4 **Explanation:** The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue. The cells visited by the first robot are set to 0. The second robot will collect 0 + 0 + 4 + 0 = 4 points. 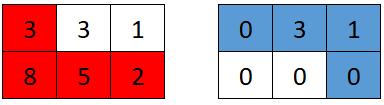**Example 2:**  **Input:** grid = \[\[3,3,1],[8,5,2]] **Output:** 4 **Explanation:** The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue. The cells visited by the first robot are set to 0. The second robot will collect 0 + 3 + 1 + 0 = 4 points. 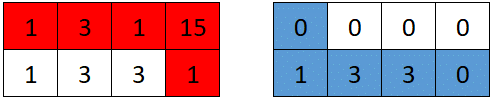**Example 3:**  **Input:** grid = \[\[1,3,1,15],[1,3,3,1]] **Output:** 7 **Explanation:** The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue. The cells visited by the first robot are set to 0. The second robot will collect 0 + 1 + 3 + 3 + 0 = 7 points. **Constraints:** * `grid.length == 2` * `n == grid[r].length` * 1 <= n <= 5 * 104 * 1 <= grid[r][c] <= 105

Constructor Summary

Constructors

Constructor	Description
Solution()

Method Summary

Modifier and Type	Method	Description
long	gridGame(int[][] grid)

Methods inherited from class java.lang.Object

clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

Constructor Details

Solution

public Solution()

Method Details

gridGame

public long gridGame(int[][] grid)