Package g2001_2100.s2045_second_minimum_time_to_reach_destination

Class Solution

java.lang.Object

g2001_2100.s2045_second_minimum_time_to_reach_destination.Solution

public class Solution
extends Object

2045 - Second Minimum Time to Reach Destination\. Hard A city is represented as a **bi-directional connected** graph with `n` vertices where each vertex is labeled from `1` to `n` ( **inclusive** ). The edges in the graph are represented as a 2D integer array `edges`, where each edges[i] = [ui, vi] denotes a bi-directional edge between vertex ui and vertex vi. Every vertex pair is connected by **at most one** edge, and no vertex has an edge to itself. The time taken to traverse any edge is `time` minutes. Each vertex has a traffic signal which changes its color from **green** to **red** and vice versa every `change` minutes. All signals change **at the same time**. You can enter a vertex at **any time** , but can leave a vertex **only when the signal is green**. You **cannot wait** at a vertex if the signal is **green**. The **second minimum value** is defined as the smallest value **strictly larger** than the minimum value. * For example the second minimum value of `[2, 3, 4]` is `3`, and the second minimum value of `[2, 2, 4]` is `4`. Given `n`, `edges`, `time`, and `change`, return _the **second minimum time** it will take to go from vertex_ `1` _to vertex_ `n`. **Notes:** * You can go through any vertex **any** number of times, **including** `1` and `n`. * You can assume that when the journey **starts** , all signals have just turned **green**. 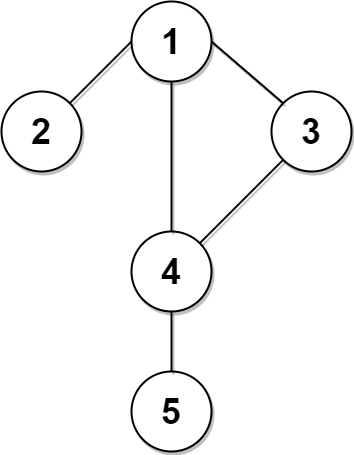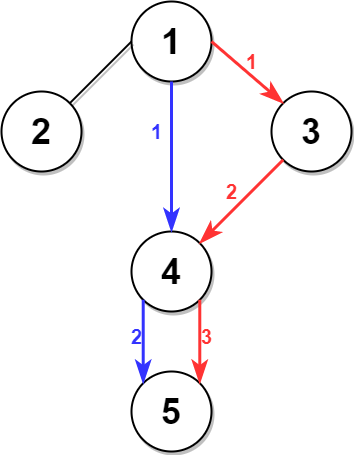**Example 1:**           **Input:** n = 5, edges = \[\[1,2],[1,3],[1,4],[3,4],[4,5]], time = 3, change = 5 **Output:** 13 **Explanation:** The figure on the left shows the given graph. The blue path in the figure on the right is the minimum time path. The time taken is: - Start at 1, time elapsed=0 - 1 -> 4: 3 minutes, time elapsed=3 - 4 -> 5: 3 minutes, time elapsed=6 Hence the minimum time needed is 6 minutes. The red path shows the path to get the second minimum time. - Start at 1, time elapsed=0 - 1 -> 3: 3 minutes, time elapsed=3 - 3 -> 4: 3 minutes, time elapsed=6 - Wait at 4 for 4 minutes, time elapsed=10 - 4 -> 5: 3 minutes, time elapsed=13 Hence the second minimum time is 13 minutes. **Example 2:**  **Input:** n = 2, edges = \[\[1,2]], time = 3, change = 2 **Output:** 11 **Explanation:** The minimum time path is 1 -> 2 with time = 3 minutes. The second minimum time path is 1 -> 2 -> 1 -> 2 with time = 11 minutes. **Constraints:** * 2 <= n <= 104 * n - 1 <= edges.length <= min(2 * 104, n * (n - 1) / 2) * `edges[i].length == 2` * 1 <= ui, vi <= n * ui != vi * There are no duplicate edges. * Each vertex can be reached directly or indirectly from every other vertex. * 1 <= time, change <= 103

Constructor Summary

Constructors

Constructor	Description
Solution()

Method Summary

Modifier and Type	Method	Description
int	secondMinimum(int n, int[][] edges, int time, int change)

Methods inherited from class java.lang.Object

clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

Constructor Details

Solution

public Solution()

Method Details

secondMinimum

public int secondMinimum(int n,
 int[][] edges,
 int time,
 int change)