Package g2001_2100.s2054_two_best_non_overlapping_events

Class Solution

java.lang.Object

g2001_2100.s2054_two_best_non_overlapping_events.Solution

public class Solution
extends Object

2054 - Two Best Non-Overlapping Events\. Medium You are given a **0-indexed** 2D integer array of `events` where events[i] = [startTimei, endTimei, valuei]. The ith event starts at startTimei and ends at endTimei, and if you attend this event, you will receive a value of valuei. You can choose **at most** **two** **non-overlapping** events to attend such that the sum of their values is **maximized**. Return _this **maximum** sum._ Note that the start time and end time is **inclusive**: that is, you cannot attend two events where one of them starts and the other ends at the same time. More specifically, if you attend an event with end time `t`, the next event must start at or after `t + 1`. 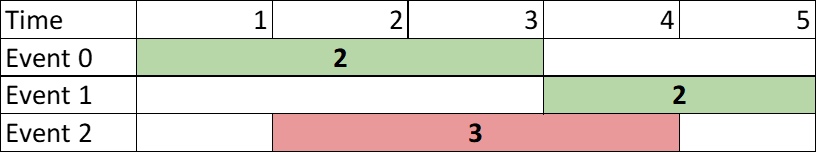**Example 1:**  **Input:** events = \[\[1,3,2],[4,5,2],[2,4,3]] **Output:** 4 **Explanation:** Choose the green events, 0 and 1 for a sum of 2 + 2 = 4. **Example 2:**  **Input:** events = \[\[1,3,2],[4,5,2],[1,5,5]] **Output:** 5 **Explanation:** Choose event 2 for a sum of 5. **Example 3:**  **Input:** events = \[\[1,5,3],[1,5,1],[6,6,5]] **Output:** 8 **Explanation:** Choose events 0 and 2 for a sum of 3 + 5 = 8. **Constraints:** * 2 <= events.length <= 105 * `events[i].length == 3` * 1 <= startTimei <= endTimei <= 109 * 1 <= valuei <= 106

Constructor Summary

Constructors

Constructor	Description
Solution()

Method Summary

Modifier and Type	Method	Description
int	maxTwoEvents(int[][] events)

Methods inherited from class java.lang.Object

clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

Constructor Details

Solution

public Solution()

Method Details

maxTwoEvents

public int maxTwoEvents(int[][] events)