Package g2001_2100.s2088_count_fertile_pyramids_in_a_land

Class Solution

java.lang.Object

g2001_2100.s2088_count_fertile_pyramids_in_a_land.Solution

public class Solution
extends Object

2088 - Count Fertile Pyramids in a Land\. Hard A farmer has a **rectangular grid** of land with `m` rows and `n` columns that can be divided into unit cells. Each cell is either **fertile** (represented by a `1`) or **barren** (represented by a `0`). All cells outside the grid are considered barren. A **pyramidal plot** of land can be defined as a set of cells with the following criteria: 1. The number of cells in the set has to be **greater than** `1` and all cells must be **fertile**. 2. The **apex** of a pyramid is the **topmost** cell of the pyramid. The **height** of a pyramid is the number of rows it covers. Let `(r, c)` be the apex of the pyramid, and its height be `h`. Then, the plot comprises of cells `(i, j)` where `r <= i <= r + h - 1` **and** `c - (i - r) <= j <= c + (i - r)`. An **inverse pyramidal plot** of land can be defined as a set of cells with similar criteria: 1. The number of cells in the set has to be **greater than** `1` and all cells must be **fertile**. 2. The **apex** of an inverse pyramid is the **bottommost** cell of the inverse pyramid. The **height** of an inverse pyramid is the number of rows it covers. Let `(r, c)` be the apex of the pyramid, and its height be `h`. Then, the plot comprises of cells `(i, j)` where `r - h + 1 <= i <= r` **and** `c - (r - i) <= j <= c + (r - i)`. Some examples of valid and invalid pyramidal (and inverse pyramidal) plots are shown below. Black cells indicate fertile cells.  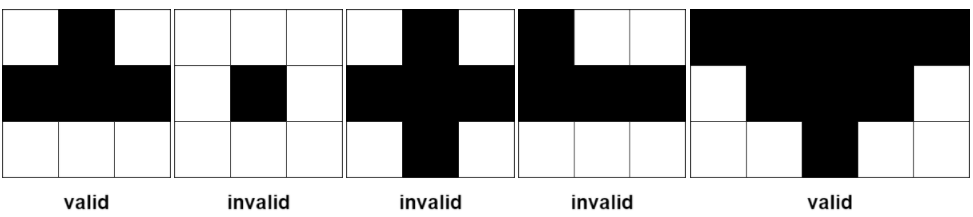Given a **0-indexed** `m x n` binary matrix `grid` representing the farmland, return _the **total number** of pyramidal and inverse pyramidal plots that can be found in_ `grid`. **Example 1:**  **Input:** grid = \[\[0,1,1,0],[1,1,1,1]] **Output:** 2 **Explanation:** The 2 possible pyramidal plots are shown in blue and red respectively. There are no inverse pyramidal plots in this grid. Hence total number of pyramidal and inverse pyramidal plots is 2 + 0 = 2. **Example 2:**  **Input:** grid = \[\[1,1,1],[1,1,1]] **Output:** 2 **Explanation:** The pyramidal plot is shown in blue, and the inverse pyramidal plot is shown in red. Hence the total number of plots is 1 + 1 = 2. **Example 3:**  **Input:** grid = \[\[1,1,1,1,0],[1,1,1,1,1],[1,1,1,1,1],[0,1,0,0,1]] **Output:** 13 **Explanation:** There are 7 pyramidal plots, 3 of which are shown in the 2nd and 3rd figures. There are 6 inverse pyramidal plots, 2 of which are shown in the last figure. The total number of plots is 7 + 6 = 13. **Constraints:** * `m == grid.length` * `n == grid[i].length` * `1 <= m, n <= 1000` * 1 <= m * n <= 105 * `grid[i][j]` is either `0` or `1`.

Constructor Summary

Constructors

Constructor	Description
Solution()

Method Summary

Modifier and Type	Method	Description
int	countPyramids(int[][] grid)

Methods inherited from class java.lang.Object

clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

Constructor Details

Solution

public Solution()

Method Details

countPyramids

public int countPyramids(int[][] grid)