Package g2301_2400.s2368_reachable_nodes_with_restrictions

Class Solution

java.lang.Object

g2301_2400.s2368_reachable_nodes_with_restrictions.Solution

public class Solution
extends Object

2368 - Reachable Nodes With Restrictions\. Medium There is an undirected tree with `n` nodes labeled from `0` to `n - 1` and `n - 1` edges. You are given a 2D integer array `edges` of length `n - 1` where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree. You are also given an integer array `restricted` which represents **restricted** nodes. Return _the **maximum** number of nodes you can reach from node_ `0` _without visiting a restricted node._ Note that node `0` will **not** be a restricted node. 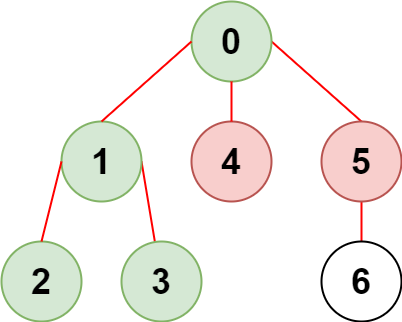**Example 1:**  **Input:** n = 7, edges = \[\[0,1],[1,2],[3,1],[4,0],[0,5],[5,6]], restricted = [4,5] **Output:** 4 **Explanation:** The diagram above shows the tree. We have that [0,1,2,3] are the only nodes that can be reached from node 0 without visiting a restricted node. 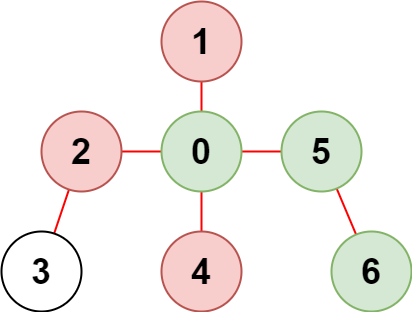**Example 2:**  **Input:** n = 7, edges = \[\[0,1],[0,2],[0,5],[0,4],[3,2],[6,5]], restricted = [4,2,1] **Output:** 3 **Explanation:** The diagram above shows the tree. We have that [0,5,6] are the only nodes that can be reached from node 0 without visiting a restricted node. **Constraints:** * 2 <= n <= 105 * `edges.length == n - 1` * `edges[i].length == 2` * 0 <= ai, bi < n * ai != bi * `edges` represents a valid tree. * `1 <= restricted.length < n` * `1 <= restricted[i] < n` * All the values of `restricted` are **unique**.

Constructor Summary

Constructors

Constructor	Description
Solution()

Method Summary

Modifier and Type	Method	Description
int	reachableNodes(int n, int[][] edges, int[] restricted)

Methods inherited from class java.lang.Object

clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

Constructor Details

Solution

public Solution()

Method Details

reachableNodes

public int reachableNodes(int n,
 int[][] edges,
 int[] restricted)