Package g1901_2000.s1971_find_if_path_exists_in_graph

Class Solution

java.lang.Object

g1901_2000.s1971_find_if_path_exists_in_graph.Solution

public class Solution
extends Object

1971 - Find if Path Exists in Graph.

Easy

There is a bi-directional graph with n vertices, where each vertex is labeled from 0 to n - 1 ( inclusive ). The edges in the graph are represented as a 2D integer array edges, where each edges[i] = [ui, vi] denotes a bi-directional edge between vertex ui and vertex vi. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.

You want to determine if there is a valid path that exists from vertex source to vertex destination.

Given edges and the integers n, source, and destination, return true if there is a valid path from source to destination, or false otherwise_._

Example 1:

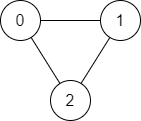
Input: n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2

Output: true

Explanation: There are two paths from vertex 0 to vertex 2: - 0 \u2192 1 \u2192 2 - 0 \u2192 2

Example 2:

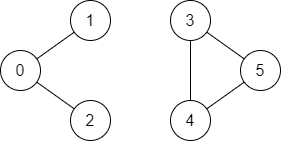
Input: n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5

Output: false

Explanation: There is no path from vertex 0 to vertex 5.

Constraints:

• 1 <= n <= 2 * 105
• 0 <= edges.length <= 2 * 105
• edges[i].length == 2
• 0 <= ui, vi <= n - 1
• ui != vi
• 0 <= source, destination <= n - 1
• There are no duplicate edges.
• There are no self edges.

Constructor Summary

Constructors

Constructor	Description
Solution()

Method Summary

Modifier and Type	Method	Description
boolean	validPath(int n, int[][] edges, int start, int end)

Methods inherited from class java.lang.Object

clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

Constructor Details

Solution

public Solution()

Method Details

validPath

public boolean validPath(int n,
 int[][] edges,
 int start,
 int end)