Package g1601_1700.s1621_number_of_sets_of_k_non_overlapping_line_segments

Class Solution

java.lang.Object
g1601_1700.s1621_number_of_sets_of_k_non_overlapping_line_segments.Solution
public class Solution extends java.lang.Object
1621 - Number of Sets of K Non-Overlapping Line Segments.

Medium

Given n points on a 1-D plane, where the ith point (from 0 to n-1) is at x = i, find the number of ways we can draw exactly k non-overlapping line segments such that each segment covers two or more points. The endpoints of each segment must have integral coordinates. The k line segments do not have to cover all n points, and they are allowed to share endpoints.

Return the number of ways we can draw k non-overlapping line segments_._ Since this number can be huge, return it modulo 109 + 7.

Example 1:

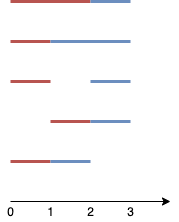
Input: n = 4, k = 2

Output: 5

Explanation: The two line segments are shown in red and blue. The image above shows the 5 different ways {(0,2),(2,3)}, {(0,1),(1,3)}, {(0,1),(2,3)}, {(1,2),(2,3)}, {(0,1),(1,2)}.

Example 2:

Input: n = 3, k = 1

Output: 3

Explanation: The 3 ways are {(0,1)}, {(0,2)}, {(1,2)}.

Example 3:

Input: n = 30, k = 7

Output: 796297179

Explanation: The total number of possible ways to draw 7 line segments is 3796297200. Taking this number modulo 109 + 7 gives us 796297179.

Constraints:

  • 2 <= n <= 1000
  • 1 <= k <= n-1

  • Constructor Summary

    Constructors
    Constructor
    Description
    Solution()
     

  • Method Summary

    Modifier and Type
    Method
    Description
    int
    numberOfSets(int n, int k)
     

    Methods inherited from class java.lang.Object

    clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

  • Constructor Details

    • Solution

      public Solution()

  • Method Details

    • numberOfSets

      public int numberOfSets(int n, int k)