Package g1901_2000.s1928_minimum_cost_to_reach_destination_in_time

Class Solution

java.lang.Object
g1901_2000.s1928_minimum_cost_to_reach_destination_in_time.Solution
public class Solution extends java.lang.Object
1928 - Minimum Cost to Reach Destination in Time.

Hard

There is a country of n cities numbered from 0 to n - 1 where all the cities are connected by bi-directional roads. The roads are represented as a 2D integer array edges where edges[i] = [xi, yi, timei] denotes a road between cities xi and yi that takes timei minutes to travel. There may be multiple roads of differing travel times connecting the same two cities, but no road connects a city to itself.

Each time you pass through a city, you must pay a passing fee. This is represented as a 0-indexed integer array passingFees of length n where passingFees[j] is the amount of dollars you must pay when you pass through city j.

In the beginning, you are at city 0 and want to reach city n - 1 in maxTime minutes or less. The cost of your journey is the summation of passing fees for each city that you passed through at some moment of your journey ( including the source and destination cities).

Given maxTime, edges, and passingFees, return the minimum cost to complete your journey, or -1 if you cannot complete it within maxTime minutes.

Example 1:

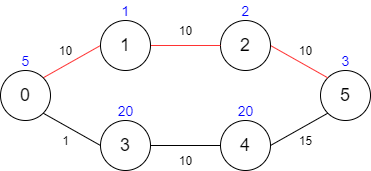
Input: maxTime = 30, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]

Output: 11

Explanation: The path to take is 0 -> 1 -> 2 -> 5, which takes 30 minutes and has $11 worth of passing fees.

Example 2:

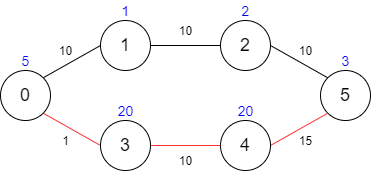
Input: maxTime = 29, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]

Output: 48

Explanation: The path to take is 0 -> 3 -> 4 -> 5, which takes 26 minutes and has $48 worth of passing fees. You cannot take path 0 -> 1 -> 2 -> 5 since it would take too long.

Example 3:

Input: maxTime = 25, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]

Output: -1

Explanation: There is no way to reach city 5 from city 0 within 25 minutes.

Constraints:

  • 1 <= maxTime <= 1000
  • n == passingFees.length
  • 2 <= n <= 1000
  • n - 1 <= edges.length <= 1000
  • 0 <= xi, yi <= n - 1
  • 1 <= timei <= 1000
  • 1 <= passingFees[j] <= 1000
  • The graph may contain multiple edges between two nodes.
  • The graph does not contain self loops.

  • Constructor Summary

    Constructors
    Constructor
    Description
    Solution()
     

  • Method Summary

    Modifier and Type
    Method
    Description
    int
    minCost(int maxTime, int[][] edges, int[] passingFees)
     

    Methods inherited from class java.lang.Object

    clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

  • Constructor Details

    • Solution

      public Solution()

  • Method Details

    • minCost

      public int minCost(int maxTime, int[][] edges, int[] passingFees)