Package g0001_0100.s0094_binary_tree_inorder_traversal

Class Solution

java.lang.Object
g0001_0100.s0094_binary_tree_inorder_traversal.Solution
public class Solution extends Object
94 - Binary Tree Inorder Traversal.

Easy

Given the root of a binary tree, return the inorder traversal of its nodes’ values.

Example 1:

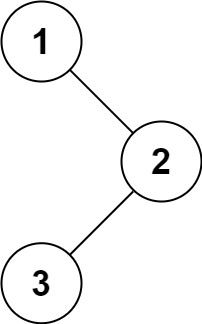
Input: root = [1,null,2,3]

Output: [1,3,2]

Example 2:

Input: root = []

Output: []

Example 3:

Input: root = [1]

Output: [1]

Example 4:

Input: root = [1,2]

Output: [2,1]

Example 5:

Input: root = [1,null,2]

Output: [1,2]

Constraints:

  • The number of nodes in the tree is in the range [0, 100].
  • -100 <= Node.val <= 100

Follow up: Recursive solution is trivial, could you do it iteratively?

To solve the “Binary Tree Inorder Traversal” problem in Java with the Solution class, follow these steps:

  1. Define a method inorderTraversal in the Solution class that takes the root of a binary tree as input and returns the inorder traversal of its nodes’ values.
  2. Implement an iterative algorithm to perform inorder traversal:
    • Initialize an empty list to store the inorder traversal result.
    • Initialize a stack to track the nodes during traversal.
    • Start with the root node and push it onto the stack.
    • While the stack is not empty:
      • Traverse down the left subtree by pushing all left child nodes onto the stack.
      • Pop the top node from the stack and add its value to the traversal result list.
      • Move to the right subtree of the popped node and repeat the process.
    • Return the traversal result list.
  3. Return the inorder traversal result list.

Here’s the implementation of the inorderTraversal method in Java:

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> inorder = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        TreeNode curr = root;
        while (curr != null || !stack.isEmpty()) {
            while (curr != null) {
                stack.push(curr);
                curr = curr.left;
            }
            curr = stack.pop();
            inorder.add(curr.val);
            curr = curr.right;
        }
        return inorder;
    }
}

This implementation performs an iterative inorder traversal of the binary tree using a stack, with a time complexity of O(N), where N is the number of nodes in the tree.

  • Constructor Details

    • Solution

      public Solution()

  • Method Details